第2話 第3講第6話プログラムの問題解明に向けての第3歩
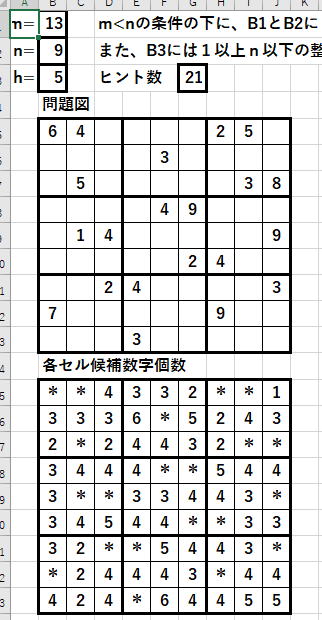
上の疑似疑似数独問題はヒント数21ですから、
第22番目のセルすなわち入力順表示の21に注目して下さい。
入力順は0から始まるので1つずれるのでしたね。
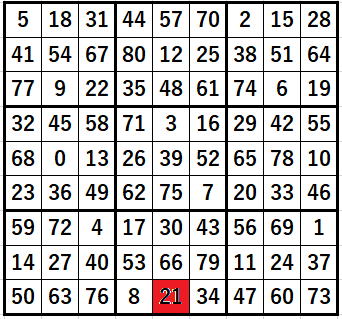
ということは、問題を解くときに最初に埋めようとしているセルは、
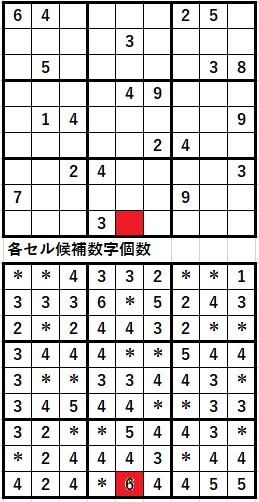
ということになります。
場合の数が多いケースの問題を解くときの大原則があります。
それは、
場合の数が少ないところから攻めよ!
です。
その大原則に反していますね。
一番場合の数が多いところから攻めようとしています。
本当は、
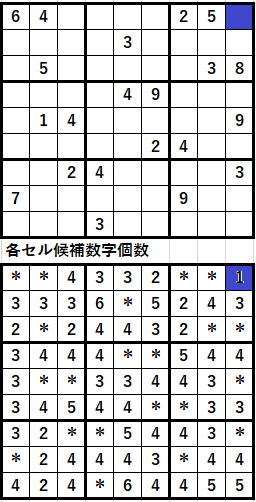
から攻めるべきです。
そして、最初に選んだ方が正解なら、
無駄な試行錯誤しなくてすみます。
この時点で、探索速度は2倍になります。
そして、入力した時点で
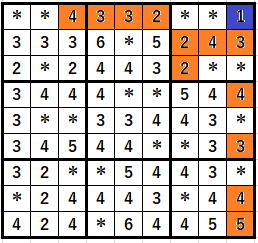
のオレンジのセルはそれぞれ1減る可能性があるのです。
81-21=60セルについて常に同じことを繰り返していけば、
どれだけ効率的に解答探索が出来るか分かりますよね。
ですから、6時間かけても(実際にはもっとでしょう)解けなかったのが、
数秒で解けてしまったりするようになるのです。
第2歩で答えが出ました。
問題を解くときのセルの入力順に問題があったのです。
問題を作るときには、最初に作った入力順で入れていかないと、
自然な数独になりませんが、
解くときには最初の座標設定で行った
入力順に囚われる必要は全くないわけです。
では、mx(i, j)が最小のセルはどうやって探したら良いのでしょうか。
Sub sds(g As Integer) '数独作成プロシージャ
Dim i As Byte, ii As Byte, iii As Byte
ii = Int(Rnd * mx(y(g), x(g)))
For i = 0 To mx(y(g), x(g))
iii = (i + ii) Mod (mx(y(g), x(g)) + 1)
p(y(g), x(g)) = rlst(y(g), x(g), iii)
If klk(g) = 1 Then '局所リスト解析プロシージャ
If g + 1 < hintosu Then
sds (g + 1)
If cn = 1 Then Exit Sub
Else
If g + 1 < n * n Then
nck (g + 1)
sds (g + 1)
・
・
nck (g + 1)は入力セル確定プロシージャです。
hintosu以上については、最初に作った座標によって進めるのではなく、
入力セル確定プロシージャによって、
その度ごとに座標y(g + 1),x(g + 1)の内容を決めて(確定させて)進めることになります。
入力セル確定プロシージャをプログラムすることによって、
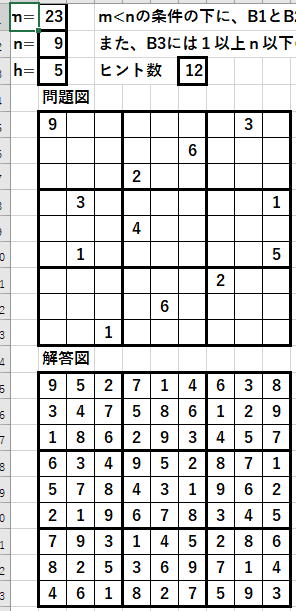

疑似数独作成ソフトVer.1を完成させて下さい。
上図の問題は、
① 解答が存在する
② 別解が存在しない
の①のみの条件を満たしている疑似数独問題です。
ヒント数16以下の数独は、
存在しないことが数学者によって証明されています。
なのに、どうして12にしてあるかと申しますと、
ヒント数を21辺りにすると1時間待っても疑似数独と解答が、
出てこないことがあるからです。
とても意外でしょう。
ヒント数が少ない方が簡単に解けるのです。
ごめんなさい。1つ重要なことを言い忘れていました。
それは、入力セル確定プロシージャを組み込む前に、
第2講の最初に行った注意
※第2講ではヒント数を20程度にするという前提で進めます。
ヒント数が多いとエラーしますし、
たまにヒント数19辺りでもエラーすることがあります。
エラーした場合は、終了を選んで下さい。
そのトラブルの解消は、第32講で行われます。
を解消しなけばならないということです。
どうして、第2講第7話の疑似疑似作成ソフト
だとヒント数が多いとエラーするのか、
あるいは少なくてもエラーしてしまう場合があるのは何故か、
これを次話で説明することにしましょう。
