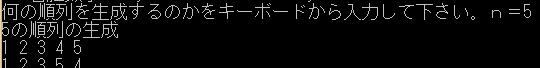
第8講 社員が自分自身に仕事を命令する=メソッドの再帰的使用
第6話 分身の術によるnの順列の生成
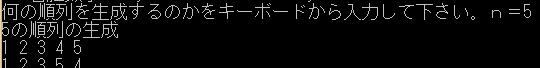
を実現するプログラム例
#! ruby -Ks
print "何の順列を生成するのかをキーボードから入力して下さい。n="
n=gets.to_i
print n,"の順列の生成\n"
def f(a,g,n)
i=1
n.times do
h=1
if g>0 then
for j in 0..(g-1)
if i==a[j] then
h=0
break
end
end
end
if h==1 then
a[g]=i
if g+1<n then
f(a,g+1,n)
else
hy(a,n)
end
end
i+=1
end
end
def hy(a,n)
i=0
n.times do
print a[i]," "
i+=1
end
print "\n"
end
a=[0]
f(a,0,n)
参考ダウンロード添付ファイル
キーボードから値を取得するには、
print "何の順列を生成するのかをキーボードから入力して下さい。n="
n=gets.to_i
のようにすればよいことを覚えて下さい。
これで、汎用的=普遍的なプログラムが出来ました。
汎用とはいろいろな方面に幅広く使えるという意味です。
また、普遍とは例外なくすべてのものに当てはまるという意味です。
プログラムを組むときには、
3の順列の生成のように個別のプログラムを組むのではなく、
nの順列の生成のように、
汎用的=普遍的なプログラムを組むようにしましょう。
さて、今回のnの順列の生成プログラムを改良していけば、
汎用的なn次魔方陣自動生成プログラムが組めます。
汎用的なプログラムにするために、
a[i]をa[i,j]と2次元配列に変更しましょう。
a=[0]
i=0
n.times do
a[i]=[[0]]
i+=1
end
でn行の2次元配列が用意できましたね。
列の方は何列であるか指定していませんが、
列の方は必要に応じてRubyの方で増やしてくれるので、
指定は必要がなかったのですね。
何故2次元配列に変更するかと申しますと、
if i==n-1 then
・・・
・・・
end
if j==n-1 then
・・・
・・・
end
のように汎用的な対応が出来るからです。
もし2次元にしていないと、
| 0 | 1 | 2 |
| 3 | 4 | 5 |
| 6 | 7 | 8 |
| 0 | 1 | 2 | 3 |
| 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 |
行合計の条件に限定しても、
3次の場合
if g==2 then
・・・
・・・
end
if g==5 then
・・・
・・・
end
if g==5 then
・・・
・・・
end
4次の場合
if g==3 then
・・・
・・・
end
if g==7 then
・・・
・・・
end
if g==11 then
・・・
・・・
end
if g==15 then
・・・
・・・
end
というように煩雑な個別の対応に終始しなければならないのに対して、
| 0 | 1 | 2 | |
| 0 | 0 | 1 | 2 |
| 1 | 3 | 4 | 5 |
| 2 | 6 | 7 | 8 |
| 0 | 1 | 2 | 3 | |
| 0 | 0 | 1 | 2 | 3 |
| 1 | 4 | 5 | 6 | 7 |
| 2 | 8 | 9 | 10 | 11 |
| 3 | 12 | 13 | 14 | 15 |
何次魔方陣に対しても
if j==n-1 then
・・・
・・・
end
の1つで済んでしまいます。
つまり汎用的=普遍的な対応ができるようになります。
では、n次魔方陣自動生成プログラムを考えましょう。
ただし、このやり方では4次魔方陣までの生成ぐらいまでしか現実的ではありません。
4次でさえすべて生成させようとしたら、
1時間は軽くかかってしまうでしょう。
5次に至っては、1万年間コンピュータに探索を続けさせても終わりません。
答は、約21億個もあるのに対して、このプログラムで1個見つけるに、
10分以上かかってしまうからです。
ですが、学習が進んでいくと6次魔方陣なら、
1秒で数百個の単位での生成が可能になります。
ですが、最速のプログラムで6次魔方陣の探索を
宇宙時間(宇宙の始まりから終わりまでの時間)続けたとしても、
6次魔方陣がいくつ存在するかの問いには答えられません。
スパコンを使った研究でも現在6次魔方陣がいくつ存在しているのかは、
解明されていません。
あなたが研究を続けて、
より高速のプログラムの開発に成功すれば、
人類史上6次魔方陣の総数をカウントした最初の人になるかも知れません。
尚、全部の魔方陣を見つける全探索でなければ、
この講義で学ぶ予定になっている最速のプログラムなら、
26次魔方陣辺りでも1秒で数百個の単位での生成が可能です。
![]()

![]()
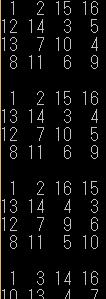
を実現させましょう。
また、行・列・対角線の合計を3次魔方陣では、
15としていましたが、
これも汎用的にnで表さなければ個別対応になります。
n次魔方陣の行などの合計は、次の式で求められます。
(1+2+3+・・・+n*n)÷n
=((1+n×n)×n×n/2)/n
=(1+n×n)×n/2
第5話へ 第7話へ
eclipse c++ 入門
魔方陣 数独で学ぶ VBA 入門
数独のシンプルな解き方・簡単な解法の研究
vc++講義へ
vba 2013 2010 2007 入門へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座へ
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
専門用語なしの C言語 C++ 入門(Visual C++ 2010で学ぶ C言語 C++ 入門)
専門用語なしの excel vba マクロ 入門 2013 2010 2007 対応講義 第1部
eclipse java 入門へ
excel 2016 vba 入門第1部へ
本サイトトップへ