第4話 例外規定
↓


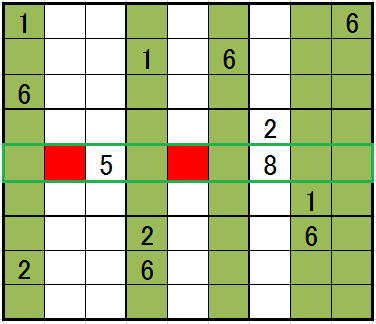
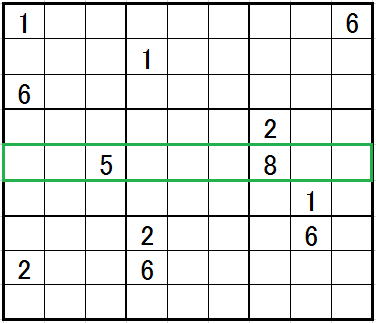
わかりやすく赤で塗ってしまいましたが、
白のセルが3つない場合でも、
3on3が成立します。
何回も申し上げてきた例外規定です。
なぜこれで3on3確定が生じてしまうかと申しますと、
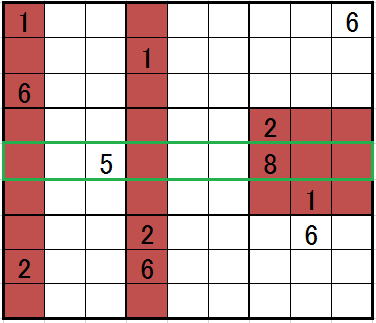
1番左のセル=1,2,6が候補になっているセルが、
仮に1だとすると、1番右側のセル=1,2のみが候補になっているセルは、
2に確定します。
すると真ん中のセルも6に確定します。
次に1番左のセルが2であるとすると、
1番左のセルが1に確定し、
真ん中のセルは6に確定します。
最後に、1番左のセルが6であるとすると、
真ん中のセルと1番左側のセルは、
1,2のみをリストとするセル群となりますから、
2on2確定すなわち相補確定が生じます。
結局どの場合を考えても、
3つのセルからなるセル群のどれかに、
1,2,6のいずれかが入ることが確定して、
3on3確定が発生します。
確定は発生するということは、
排除も発生します。
ただのリスト構造解析なら、空白のセルのリスト構造は順に、
{7,9,3,4,6,2,1,8,5}
{1,2,3,4,9,6,7,8,5}
{8,7,3,4,9,2,6,1,5}
{8,7,3,4,9,2,6,1,5}
{7,9,3,4,2,6,1,8,5}
{9,7,3,4,1,2,6,8,5}
ですが、1,2,6排除される結果、
{7,9,3,4,6,2,1,8,5}
{7,9,3,4,6,2,1,8,5}
{8,7,3,4,9,2,6,1,5}
{8,7,3,4,9,2,6,1,5}
{7,9,3,4,2,6,1,8,5}
{9,7,3,4,1,2,6,8,5}
となり、2番目のセルのリスト構造が、
{1,2,3,4,9,6,7,8,5}
から
{7,9,3,4,6,2,1,8,5}
へと大躍進を遂げるわけです。
3つもリストから外されたのですから、
3on3確定による排除による威力の大きさが分かります。
確定法で解くにはとにかくmx(i, j)のどこかを0にもっていくしかないわけです。
排除によってリスト数を減らし続ける・・・・
確定法すなわち理詰めで解くには、これしかないわけです。
第4話まで読んできて、
なるほど
3on3の確定と排除の解析は、
大変に難しい課題であることが見えてきたのではないでしょうか。
佐藤(私の名前です。)さん、3on3程度で挫けそうになるなんてだらしない・・・
とお思いの方もなるど、
苦戦は仕方がないと思って下さったのではないでしょうか。
そして、口頭ではなく文章で説明することが、
窮極の難題であることについても理解して下さったのではないでしょうか。
本当に一時の心境は







 だったし、
だったし、絶望とさえ思いました。
でも何とか乗り越えることが出来ましたので、
第4部の講義が続けられているわけです。
