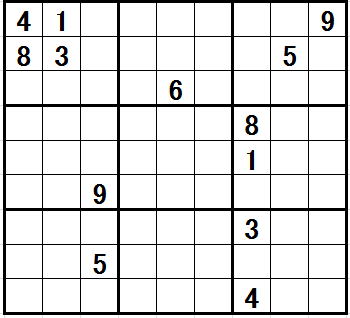
どこが相補確定になっているか考えて下さい。
そして、それによる排除には意味があるでしょうか。
答は例によって30行下。
答
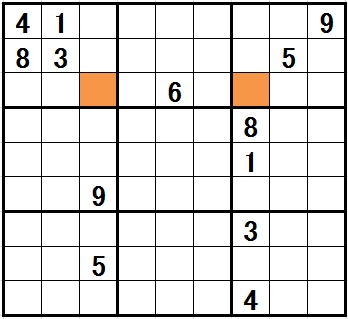
オレンジのセルが相補確定の起きるセルです。
左側のオレンジのセルは、
行の条件から6が外され、
列の条件から9と5が外され、
ブロックの条件から4,1,8,3が外されますので、
左のオレンジに入る可能性があるのは、
2と7のみです。
同様に、右側のセルは、
行の条件から6が外され、
列の条件から8,1,3,4が外され、
ブロックの条件から9と5が外されますので、
右側のオレンジに入る可能性があるのは、
2と7のみです。
2つのセルに対して2と7のみがリストされますから、
2と7による相補確定が生じ、
オレンジのセル群に2と7のいずれかが入ることが確定します。
そして、その結果
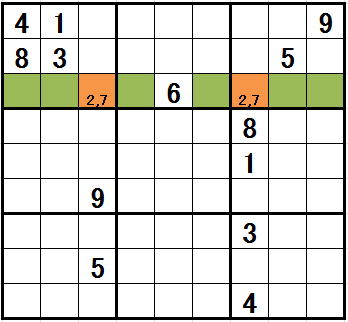
緑のセルのリストから2と7が外されます。
相補確定排除が起きる前のリスト構造は、
左から
{7,2,5,9,6,3,8,1,4},mx(2, 0) = 3
{7,2,5,9,6,3,8,1,4},mx(2, 1) = 3
{1,2,3,4,5,9,7,8,6},mx(2, 3) = 7
{1,2,3,4,5,9,7,8,6},mx(2, 5) = 7
{1,2,3,4,8,7,9,5,6},mx(2, 7) = 5
{1,2,3,4,8,7,9,5,6},mx(2, 8) = 5
であったものが、一気に2つずつmxが小さくなり、
{5,9,7,2,6,3,8,1,4},mx(2, 0) = 1
{5,9,7,2,6,3,8,1,4},mx(2, 1) = 1
{1,8,3,4,5,9,7,2,6},mx(2, 3) = 5
{1,8,3,4,5,9,7,2,6},mx(2, 5) = 5
{1,2,8,4,7,2,9,5,6},mx(2, 7) = 3
{1,2,8,4,7,2,9,5,6},mx(2, 8) = 3
今回の事例は、確定セル群への確定は起きていますが、
確定セルが発生しているわけでありません。
しかし、それでも確定セルに向けての大前進がなされたわけです。
特に、
{5,9,7,2,6,3,8,1,4},mx(2, 0) = 1
{5,9,7,2,6,3,8,1,4},mx(2, 1) = 1
あと1つ候補数字数を減らせば、確定セルとなります。
確定セルを発生させるには、
リスト個数を減らしていけばよいわけです。
今回、プログラムに入る前に3話も投入してしまいました。
何故かは、皆さんお分かりですよね。
プログラミングするためには、
自分が相手にしている事象・対象の内容を正確に把握する必要があるのでしたね。
敵を知らずに敵の攻略は不可能なのです。
数独=ナンプレを知らずにして、
数独=ナンプレの問題解法ソフトや問題生成アプリを作ることは不可能です。
vba 2016 入門の講義でもすでに触れたことがあるかも知れませんが、
日産で、一番最初にエンジン制御プログラムを開発した人は、
車を愛し、
エンジンの構造やエンジンにおけるガソリンの燃焼の仕組みに精通していたそうです。
読者の中にプログラマーを目指している人がもしいらっしゃったら、
プログラミングだけではなく、
数学・物理学・化学はもちろんのこと、
経済や家庭科などにも興味を持ちしっかり勉強されることをお勧めします。
おいしいご飯の炊き方を知らない人には、
炊飯ジャー制御プログラムを組むことはできません。
プログラマーには経営管理ソフトを組むなどの様々な仕事が依頼されます。
ですから、プログラマーはプログラムの専門知識だけでなく、
幅広い教養を必要とするのです。
もちろんすべての学問に精通することは不可能ですが、
基礎知識を持っていれば、
依頼された領域について調べて理解することは容易に出来ます。
基礎をもっていない人は、ネットで調べたり、書籍で調べたりしても、
内容を理解できません。
学生さん、今学校で学んでいる教科を選り好みせずに、
すべてに興味を持って学習に取り組みましょう。
特に、数学の学習はプログラマーには絶対の条件ですよ。
最近話題になっているAIも高度な数学を応用しているのです。
哲学者のライプニッツは、普遍数学を構想していました。
普遍数学とは、
数学が発展していけばあらゆる領域の問題が数学の対象になるというものです。
ライプニッツは、哲学の問題も、法学の問題も、恋愛の問題も、
すべて、方程式で解けるようになると考えていました。
AIの時代になるまで、
ライプニッツの考えは妄想だとして斥ける人も多かったでしょうが、
高度な数学を応用したAIが、
囲碁で世界NO.1の棋士を破り、
将棋名人を破り、
小説を書き、作曲をし、絵画を描くのです。
しかも、作曲のレベルは世界的に有名な作曲家の作曲のレベルを超えているのです。
あるコンサート会場で、
世界的に有名な作曲家人が作曲した2曲とAIが作曲した曲の合計3曲について、
作曲者を伏せて演奏してから、
どの曲が一番感動したかのアンケートを採ったら、
AIの作曲した曲が1番になったそうです。
絵画や小説のレベルもやがては人間を越えるでしょう。
ライプニッツの考えが正しいことが証明されようとしているのです。
それでは、皆さんVer.2に1:1対応確定と排除を組み込んで行くことにしましょう。
