第4話 疑似数独作成ソフトVer.1
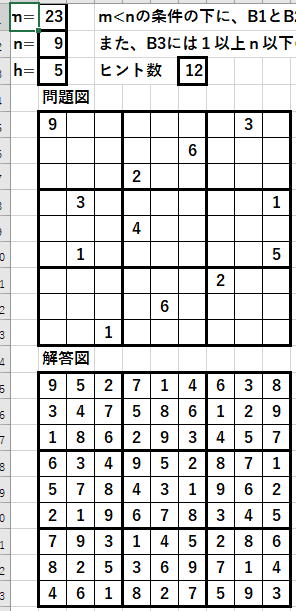

を実現するプログラム例
Dim m As Integer, n As Integer, h As Integer
Dim p(8, 8) As Byte, mx(8, 8) As Byte, rlst(8, 8, 8) As Byte
'pは数独を収納する配列
'mxは各セルの候補数字の個数を収納する配列
'rlstは候補数字を収納する配列
Dim y(80) As Byte, x(80) As Byte
Dim a(8, 8) As Integer
Dim hintosu As Byte, rn As Byte
Dim cn As Integer
Dim cmx(80, 8, 8) As Byte
Dim crlst(80, 8, 8, 8) As Byte
Dim hth(80, 8, 8) As Byte
Private Sub CommandButton1_Click()
Rnd (-1)
Dim hj As Single
hj = Timer
Randomize hj
CommandButton2_Click
m = Cells(1, 2)
n = Cells(2, 2)
h = Cells(3, 2)
rn = Int(Sqr(n))
hintosu = Cells(3, 7)
zlk '全体リスト構造解析プロシージャ
zys '座標作成プロシージャ
sds (0) '数独作成プロシージャ
' If kensyou(a, n) = 1 Then
' Cells(4, 2) = "すべての数字が網羅されています。"
' Else
' Cells(4, 2) = "一部の数字しか入っていません。"
' End If
'全体リスト構造解析表示プロシージャ 正しいことが確認できた際にはこれを外す。
'全体リスト構造解析表示プロシージャを入れておくと処理にかなり時間を要する。
'hyouji1
hyouji2
Cells(6, 12) = "数独作成にかかった時間は"
Cells(7, 12) = Timer - hj
Cells(8, 12) = "秒です。"
Range("A1").Select
End Sub
Sub zlk() '全体リスト構造解析プロシージャ
Dim i As Integer, j As Integer, k As Integer, l As Integer
cn = 0
For i = 0 To n - 1
For j = 0 To n - 1
mx(i, j) = n - 1
p(i, j) = 0
For k = 0 To n - 1
rlst(i, j, k) = k + 1
Next
Next
Next
For i = 0 To n * n - 1
For j = 0 To n - 1
For k = 0 To n - 1
hth(i, j, k) = 0
Next
Next
Next
End Sub
Sub zys() '座標作成プロシージャ
Dim i As Byte
Dim s As Byte, t As Byte
For i = 0 To n * n - 1
s = Int(i / n)
t = i Mod n
a(s, t) = (h + i * m) Mod (n * n)
y(a(s, t)) = s
x(a(s, t)) = t
Next
End Sub
Sub sds(g As Integer) '数独作成プロシージャ
Dim i As Byte, ii As Byte, iii As Byte
ii = Int(Rnd * mx(y(g), x(g)))
For i = 0 To mx(y(g), x(g))
iii = (i + ii) Mod (mx(y(g), x(g)) + 1)
p(y(g), x(g)) = rlst(y(g), x(g), iii)
If klk(g) = 1 Then '局所リスト解析プロシージャ
If g + 1 < hintosu Then
sds (g + 1)
If cn = 1 Then Exit Sub
Else
If g + 1 < n * n Then
nck (g + 1)
sds (g + 1)
If cn = 1 Then Exit Sub
Else
hyouji '問題表示プロシージャ
cn = cn + 1
Exit Sub
End If
End If
End If
hukugen (g)
Next
p(y(g), x(g)) = 0
End Sub
Sub nck(g As Byte)
Dim i As Byte, j As Byte, mn As Byte, ik As Byte, jk As Byte
mn = 100
For i = 0 To n - 1
For j = 0 To n - 1
If p(i, j) = 0 Then
If mn > mx(i, j) Then
mn = mx(i, j)
ik = i
jk = j
If mn = 0 Then
y(g) = ik
x(g) = jk
Exit Sub
End If
End If
End If
Next
Next
y(g) = ik
x(g) = jk
End Sub
Function klk(g As Integer) '局所リスト解析プロシージャ
Dim i As Byte, j As Byte, k As Byte, w As Byte
For i = 0 To n - 1
For j = 0 To n - 1
hth(g, i, j) = 0
Next
Next
For i = 0 To n - 1
If p(y(g), i) = 0 Then
For j = 0 To mx(y(g), i)
If p(y(g), x(g)) = rlst(y(g), i, j) Then
If mx(y(g), i) = 0 Then
klk = 0
Exit Function
End If
hth(g, y(g), i) = 1
For k = 0 To n - 1
crlst(g, y(g), i, k) = rlst(y(g), i, k)
Next
cmx(g, y(g), i) = mx(y(g), i)
w = rlst(y(g), i, j)
rlst(y(g), i, j) = rlst(y(g), i, mx(y(g), i))
rlst(y(g), i, mx(y(g), i)) = w
mx(y(g), i) = mx(y(g), i) - 1
Exit For
End If
Next
End If
Next
For i = 0 To n - 1
If p(i, x(g)) = 0 Then
For j = 0 To mx(i, x(g))
If p(y(g), x(g)) = rlst(i, x(g), j) Then
If mx(i, x(g)) = 0 Then
klk = 0
Exit Function
End If
hth(g, i, x(g)) = 1
For k = 0 To n - 1
crlst(g, i, x(g), k) = rlst(i, x(g), k)
Next
cmx(g, i, x(g)) = mx(i, x(g))
w = rlst(i, x(g), j)
rlst(i, x(g), j) = rlst(i, x(g), mx(i, x(g)))
rlst(i, x(g), mx(i, x(g))) = w
mx(i, x(g)) = mx(i, x(g)) - 1
Exit For
End If
Next
End If
Next
Dim ybs As Byte, xbs As Byte
Dim isy As Byte, ia As Byte
ybs = rn * Int(y(g) / rn)
xbs = rn * Int(x(g) / rn)
For i = 0 To n - 1
isy = Int(i / rn)
ia = i Mod rn
If ybs + isy <> y(g) And xbs + ia <> x(g) And p(ybs + isy, xbs + ia) = 0 Then
For j = 0 To mx(ybs + isy, xbs + ia)
If p(y(g), x(g)) = rlst(ybs + isy, xbs + ia, j) Then
If mx(ybs + isy, xbs + ia) = 0 Then
klk = 0
Exit Function
End If
hth(g, ybs + isy, xbs + ia) = 1
For k = 0 To n - 1
crlst(g, ybs + isy, xbs + ia, k) = rlst(ybs + isy, xbs + ia, k)
Next
cmx(g, ybs + isy, xbs + ia) = mx(ybs + isy, xbs + ia)
w = rlst(ybs + isy, xbs + ia, j)
rlst(ybs + isy, xbs + ia, j) = rlst(ybs + isy, xbs + ia, mx(ybs + isy, xbs + ia))
rlst(ybs + isy, xbs + ia, mx(ybs + isy, xbs + ia)) = w
mx(ybs + isy, xbs + ia) = mx(ybs + isy, xbs + ia) - 1
Exit For
End If
Next
End If
Next
klk = 1
End Function
Sub hukugen(g As Integer)
Dim i As Byte, j As Byte, ybs As Byte, xbs As Byte, isy As Byte, ia As Byte
For i = 0 To n - 1
If i <> x(g) And p(y(g), i) = 0 Then
If hth(g, y(g), i) = 1 Then
For j = 0 To n - 1
rlst(y(g), i, j) = crlst(g, y(g), i, j)
Next
mx(y(g), i) = cmx(g, y(g), i)
End If
End If
Next
For i = 0 To n - 1
If i <> y(g) And p(i, x(g)) = 0 Then
If hth(g, i, x(g)) = 1 Then
For j = 0 To n - 1
rlst(i, x(g), j) = crlst(g, i, x(g), j)
Next
mx(i, x(g)) = cmx(g, i, x(g))
End If
End If
Next
ybs = rn * Int(y(g) / rn)
xbs = rn * Int(x(g) / rn)
For i = 0 To n - 1
isy = Int(i / rn)
ia = i Mod rn
If ybs + isy <> y(g) And xbs + ia <> x(g) And p(ybs + isy, xbs + ia) = 0 Then
If hth(g, ybs + isy, xbs + ia) = 1 Then
For j = 0 To n - 1
rlst(ybs + isy, xbs + ia, j) = crlst(g, ybs + isy, xbs + ia, j)
Next
mx(ybs + isy, xbs + ia) = cmx(g, ybs + isy, xbs + ia)
End If
End If
Next
End Sub
Sub hyouji() '問題表示プロシージャ
Dim i As Integer
For i = 0 To hintosu - 1
Cells(5 + y(i), 2 + x(i)) = p(y(i), x(i))
Next
End Sub
Sub hyouji2() '問題表示プロシージャ
Dim i As Integer
For i = 0 To n * n - 1
Cells(15 + y(i), 2 + x(i)) = p(y(i), x(i))
Next
End Sub
'以下全体リスト構造解析表示プロシージャ 正しいことが確認できた際にもプロシージャ自体は残しておく
'この後のプログラムの進展の際に何回も利用するするから
Sub hyouji1()
Dim i As Integer, j As Integer
For i = 0 To n - 1
For j = 0 To n - 1
If p(i, j) = 0 Then
For k = 0 To n - 1
Cells(15 + i, 2 + 10 * j + k) = rlst(i, j, k)
Next
For k = 0 To mx(i, j)
'以下は、マクロの記録から学んだもの
Cells(15 + i, 2 + 10 * j + k).Select
With Selection.Interior
.Pattern = xlSolid
.PatternColorIndex = xlAutomatic
.ThemeColor = xlThemeColorAccent5
.TintAndShade = 0
.PatternTintAndShade = 0
End With
'以上は、マクロの記録から学んだもの
Next
For k = mx(i, j) + 1 To n - 1
'以下は、マクロの記録から学んだもの
Cells(15 + i, 2 + 10 * j + k).Select
With Selection.Interior
.Pattern = xlSolid
.PatternColorIndex = xlAutomatic
.ThemeColor = xlThemeColorAccent2
.TintAndShade = 0.388845066682843
.PatternTintAndShade = 0
End With
'以上は、マクロの記録から学んだもの
Next
Else
For k = 0 To n - 1
Cells(15 + i, 2 + 10 * j + k) = "*"
Next
End If
Next
Next
End Sub
Function kensyou(a() As Integer, n As Integer)
Dim b(80) As Byte, i As Integer, j As Integer
For i = 0 To n * n - 1
b(i) = 0
Next
For i = 0 To n - 1
For j = 0 To n - 1
b(a(i, j)) = 1
Next
Next
For i = 0 To n - 1
If b(i) = 0 Then
kensyou = 0
Exit Function
End If
Next
kensyou = 1
End Function
Private Sub CommandButton2_Click()
Rows("5:13").Select
Selection.ClearContents
Rows("15:23").Select
Selection.ClearContents
' Rows("15:35").Select
' Selection.Delete
Range("A1").Select
End Sub
参考ダウンロード添付ファイル
ヒント数を21辺りにしても、
0.1秒ぐらいで疑似数独と解答ができる場合もありますが、
待てども待てども結果が出てこないこともあります。
忍耐強く待ち続ければ、必ず結果が出てきますが、
実験していませんが、1時間以上かかる場合もあるでしょう。
これでは、疑似数独作成ソフトとはいえません。
そこで、Ver.2の開発に取りかかりたいと思います。
2つ目の工夫とは何か?
時間がかかってしまうのは、
最初にヒント数に基づいて配置した数字からなる問題が、
解のない問題になっているケースが考えられます。
解がないことを証明するのはかなり時間がかかるのです。
② 別解がない
の条件確認も同様に時間がかかるのです。
ですから疑似数独作成ソフトと数独作成ソフトには大きな隔たりがあります。
最後の疑似を取るにはやはり大跳躍が必要なのです。
解がなければ最初の配置(問題自体)も
試行錯誤していじるようになっていますので、
待ち続ければ必ず疑似数独と解答が表示されるわけですが、
配置を深いところまでやり直さなければならないときには、
膨大な時間がかかってしまうのです。
ならば、どのように改善すべきでしょうか。
