第1話 疑似疑似数独作成ソフトに問題を解かせる
第3講の目的は、

数独作成アプリVer.1を開発することです。
第3講 数独作成アプリVer.1開発その1
第1話 疑似疑似数独作成ソフトに問題を解かせる
第3講の目的は、

数独作成アプリVer.1を開発することです。
これを開発するためには、第31講第7話で作った疑似疑似数独作成ソフトから、
2つの疑似を取らなければなりませんが、
① 解答が存在する
② 別解が存在しない
の2つの条件をクリアしなければなりません。
第32講では
第31講第7話の 参考ダウンロード添付ファイル
に改良を加えていくことによってクリアを考えます。
その改良によって、ヒント数が多いとエラーを起こす場合があるという、
第7話のソフトの欠陥も同時に解消されます。
① 解答が存在する
を示すには、自分が作った問題を解かなければなりません。
問題を試行錯誤法=仮定法=背理法ではなく、理詰めで解く場合にも
全体リスト構造解析は避けては通れません。
仮定法を使わずに解く方法を私は確定法と呼びます。
その理由は、空欄の中に必ず少なくとも1つは1つの数字に確定するセルがあるということです。
様々な方法を駆使して、リストを絞り込んでいって、
mx(i, j) = 0になるセルを見つけていけば、
仮定法は使わなくて良いわけです。
このとき、リスト構造は例えば次のようになっているわけです。
{8,2,3,1,5,4,9,7,6}
つまり、そのセルは8に確定しているのです。
mx(i, j) = 4で
{8,2,3,1,5,4,9,7,6}
となっていれば、可能性は8,2,3,1,5あって試行錯誤になってしまうわけです。
8でだめなら2を試し、2でだめなら3を試し、・・・
となってしまいます。
まさに、仮定法=仮置きの方法です。
ですが、現時点では

候補数字個数が1つつまりmx(i, j) = 0になっているセルは1つもありません。
青い部分が1つになっているセルはないですよね。
今の数独のルールからリスト構造を作るというだけでは、
いつでも確定できるセルがある状態にするのは不可能と言ってよいでしょう。
ですから、今の段階では試行錯誤法で解くしかないわけです。
試行錯誤法で解く際に
第31講第7話の 参考ダウンロード添付ファイル
には大きな問題があります。
その問題まず解消しなければなりません。
実は、もう一つ大きな問題があります。
それは作成時間です。上でいった大きな問題を解消できても、
時間の壁が立ちはだかります。
ですから、第32講では大きな問題を2つクリアしなければならないのです。
これからは、時間と戦いになりますので、時間計測機能を
第2講第7話の 参考ダウンロード添付ファイル
につけ加えて下さい。
ただし、全体リスト構造表示機能は'
'hyouji1
を加えることによって、一時的に外しておいて下さい。
また、
If kensyou(a, n) = 1 Then
Cells(4, 2) = "すべての数字が網羅されています。"
Else
Cells(4, 2) = "一部の数字しか入っていません。"
End If
の部分も要りませんので全部注釈文にしておきましょう。
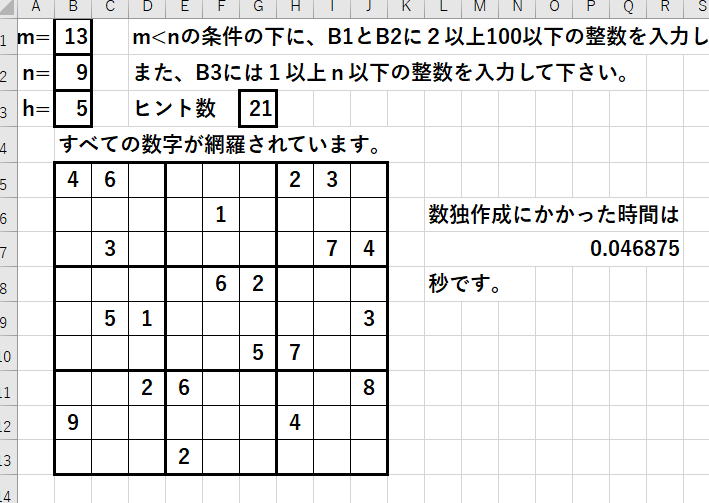
シートの方は、手作業で作って下さい。
eclipse c++ 入門
魔方陣 数独(ナンプレ)で学ぶ VBA 入門
数独(ナンプレ)のシンプルな解き方・簡単な解法の研究
vc++講義へ
excel 2013 2010 2007 vba入門へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座へ
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
専門用語なしの C言語 C++ 入門(Visual C++ 2010で学ぶ C言語 C++ 入門)
専門用語なしの excel vba マクロ 入門 2013 2010 2007 対応講義 第1部
eclipse java 入門へ
excel 2016 vba 入門へ
小学生からエンジニアまでのRuby入門へ
本サイトトップへ