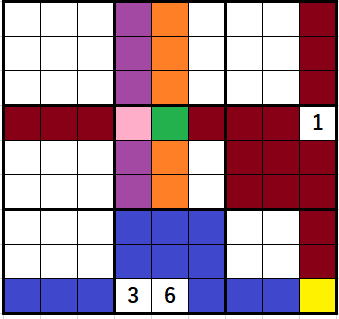
の黄色のセルを例にどのようにリスト構造解析が行われているか、
トレースしてみましょう。
6が入ったときのリスト構造解析ですから、
黄色のセルのは解析は
For i = 0 To n - 1
If p(y(g), i) = 0 Then
For j = 0 To mx(y(g), i)
If p(y(g), x(g)) = rlst(y(g), i, j) Then
w = rlst(y(g), i, j)
rlst(y(g), i, j) = rlst(y(g), i, mx(y(g), i))
rlst(y(g), i, mx(y(g), i)) = w
mx(y(g), i) = mx(y(g), i) - 1
Exit For
End If
Next
End If
Next
の部分が行っています。座標に具体的な数字を代入すると、
If p(8, 8) = 0 Then
For j = 0 To mx(8, 8)
If p(8, 4) = rlst(8, 8, j) Then
w = rlst(8, 8, j)
rlst(8, 8, j) = rlst(8, 8, mx(8, 8))
rlst(8, 8, mx(8, 8)) = w
mx(8, 8) = mx(8, 8) - 1
Exit For
End If
Next
End If
6が入る前の黄色セルのリスト構造は、

{8,2,9,4,5,6,7,1,3}
mx(8, 8) = 6
となっていますから、
For j = 0 To mx(8, 8)
If p(8, 4) = rlst(8, 8, j) Then
は
For j = 0 To 6
If p(8, 4) = rlst(8, 8, j) Then
で、6が何番目にリストされているか探しています。
0から数えることに注意して数えると、jが5の場合です。
w = rlst(8, 8, 5)
rlst(8, 8, 5) = rlst(8, 8, 6)
rlst(8, 8, mx(8, 8)) = w
この3行で行っていることは、6,7の交換です。
{8,2,9,4,5,7,6,1,3}
そして、
mx(8, 8) = mx(8, 8) - 1
によって、mx(8, 8) = 5となり、有効範囲が1つ減って、
{8,2,9,4,5,7,6,1,3}
となります。
このプロシージャでは
この3が入った場合
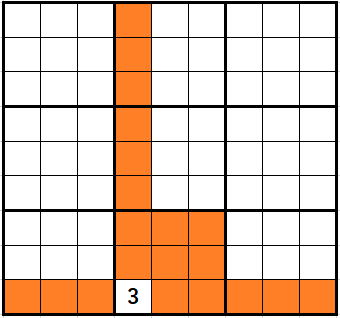
オレンジのセルについて
{1,2,3,4,5,6,7,8,9}
↓
{1,2,9,4,5,6,7,8,3}
↓
{1,2,9,4,5,6,7,8,3}
としていますが、
{1,2,3,4,5,6,7,8,9}
↓
{1,2,4,5,6,7,8,9,3}
↓
{1,2,4,5,6,7,8,9,3}
とする方法も考えられます。
下の方法を選ばなかったのは、
下の方法だと、
有効範囲の中では、いつでも小さい順になっています。
ランダムに選びますから、
これでも良かったかも知れませんが、
今回の方式は進めば進むほど順番がランダムになります。
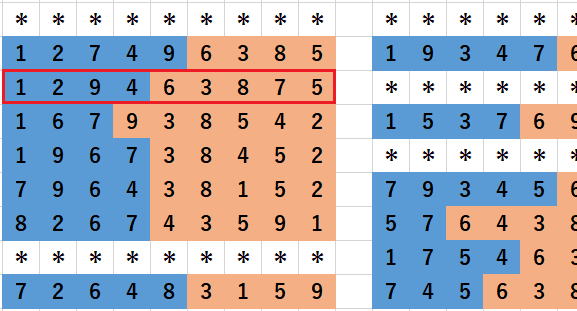
すると有効範囲の中からランダムに選びますので、
2重にランダムに選ぶことになります。
上の方式にすれば2重ランダムになり、
ランダム性が上がり、より自然な数独が出来るのではと考えてそうしました。
ただ、プログラミングのおもしろさと難しさは、
実際に試してみると、頭の中で想定していた結果と違っていたりします。
{1,2,3,4,5,6,7,8,9}
↓
{1,2,9,4,5,6,7,8,3}
↓
{1,2,9,4,5,6,7,8,3}
と
{1,2,3,4,5,6,7,8,9}
↓
{1,2,4,5,6,7,8,9,3}
↓
{1,2,4,5,6,7,8,9,3}
のどちらの方式の方が良い結果を導くかは、
やってみなければ分かりません。
今回作成までの時間を計測していませんが、
時間計測を組み込んで、
どちらの方式が勝るのか、
是非ともご自分で試されることをお勧めします。
さて、以上で第2講は終了とします。
次の課題は、
① 解答が存在する
② 別解が存在しない
の2つを満たさせることです。
①が満たされれば、疑似が1個取れて
疑似数独作成ソフトになりますし、
更に②が満たされれば、疑似が全部取れて、
数独作成ソフトの一応の完成となります。
一応がつくのは、このソフトは残念ながら試行錯誤法で解答を作っていますので、
仮定法を使わなければ解けないクオリティーの低い問題しか作れないからです。
