第7話 疑似疑似数独作成ソフト

を実現するプログラム例
Dim p(8, 8) As Byte, mx(8, 8) As Byte, rlst(8, 8, 8) As Byte
'pは数独を収納する配列
'mxは各セルの候補数字の個数を収納する配列
'rlstは候補数字を収納する配列
Dim y(81) As Byte, x(81) As Byte
Dim a(8, 8) As Integer
Dim hintosu As Byte, rn As Byte
Dim cn As Integer
Private Sub CommandButton1_Click()
Rnd (-1)
Randomize Timer
CommandButton2_Click
m = Cells(1, 2)
n = Cells(2, 2)
h = Cells(3, 2)
rn = Int(Sqr(n))
hintosu = Cells(3, 7)
zlk '全体リスト構造解析プロシージャ
zys '座標作成プロシージャ
sds (0) '数独作成プロシージャ
If kensyou(a, n) = 1 Then
Cells(4, 2) = "すべての数字が網羅されています。"
Else
Cells(4, 2) = "一部の数字しか入っていません。"
End If
'全体リスト構造解析表示プロシージャ 正しいことが確認できた際にはこれを外す。
'全体リスト構造解析表示プロシージャを入れておくと処理にかなり時間を要する。
hyouji1
Range("A1").Select
End Sub
Sub zlk() '全体リスト構造解析プロシージャ
Dim i As Integer, j As Integer, k As Integer
cn = 0
For i = 0 To n - 1
For j = 0 To n - 1
mx(i, j) = n - 1
p(i, j) = 0
For k = 0 To n - 1
rlst(i, j, k) = k + 1
Next
Next
Next
End Sub
Sub zys() '座標作成プロシージャ
Dim i As Byte
Dim s As Byte, t As Byte
For i = 0 To n * n - 1
s = Int(i / n)
t = i Mod n
a(s, t) = (h + i * m) Mod (n * n)
y(a(s, t)) = s
x(a(s, t)) = t
Next
End Sub
Sub sds(g As Integer) '数独作成プロシージャ
Dim i As Byte, ii As Byte, iii As Byte
ii = Int(Rnd * mx(y(g), x(g)))
For i = 0 To mx(y(g), x(g))
iii = (i + ii) Mod (mx(y(g), x(g)) + 1)
p(y(g), x(g)) = rlst(y(g), x(g), iii)
klk (g) '局所リスト構造解析プロシージャ
If g + 1 < hintosu Then
sds (g + 1)
If cn = 1 Then Exit Sub
Else
hyouji '問題表示プロシージャ
cn = cn + 1
Exit Sub
End If
Next
p(y(g), x(g)) = 0
End Sub
Sub klk(g As Integer) '局所リスト構造解析プロシージャ
Dim i As Byte, j As Byte, k As Byte, w As Byte
For i = 0 To n - 1
If p(y(g), i) = 0 Then
For j = 0 To mx(y(g), i)
If p(y(g), x(g)) = rlst(y(g), i, j) Then
w = rlst(y(g), i, j)
rlst(y(g), i, j) = rlst(y(g), i, mx(y(g), i))
rlst(y(g), i, mx(y(g), i)) = w
mx(y(g), i) = mx(y(g), i) - 1
Exit For
End If
Next
End If
Next
For i = 0 To n - 1
If p(i, x(g)) = 0 Then
For j = 0 To mx(i, x(g))
If p(y(g), x(g)) = rlst(i, x(g), j) Then
w = rlst(i, x(g), j)
rlst(i, x(g), j) = rlst(i, x(g), mx(i, x(g)))
rlst(i, x(g), mx(i, x(g))) = w
mx(i, x(g)) = mx(i, x(g)) - 1
Exit For
End If
Next
End If
Next
Dim ybs As Byte, xbs As Byte
Dim isy As Byte, ia As Byte
ybs = rn * Int(y(g) / rn)
xbs = rn * Int(x(g) / rn)
For i = 0 To n - 1
isy = Int(i / rn)
ia = i Mod rn
If ybs + isy <> y(g) And xbs + ia <> x(g) And p(ybs + isy, xbs + ia) = 0 Then
For j = 0 To mx(ybs + isy, xbs + ia)
If p(y(g), x(g)) = rlst(ybs + isy, xbs + ia, j) Then
w = rlst(ybs + isy, xbs + ia, j)
rlst(ybs + isy, xbs + ia, j) = rlst(ybs + isy, xbs + ia, mx(ybs + isy, xbs + ia))
rlst(ybs + isy, xbs + ia, mx(ybs + isy, xbs + ia)) = w
mx(ybs + isy, xbs + ia) = mx(ybs + isy, xbs + ia) - 1
Exit For
End If
Next
End If
Next
End Sub
Sub hyouji() '問題表示プロシージャ
Dim i As Integer
For i = 0 To hintosu - 1
Cells(5 + y(i), 2 + x(i)) = p(y(i), x(i))
Next
End Sub
'以下全体リスト構造解析表示プロシージャ 正しいことが確認できた際にもプロシージャ自体は残しておく
'この後のプログラムの進展の際に何回も利用するするから
Sub hyouji1()
Dim i As Integer, j As Integer
For i = 0 To n - 1
For j = 0 To n - 1
If p(i, j) = 0 Then
For k = 0 To n - 1
Cells(15 + i, 2 + 10 * j + k) = rlst(i, j, k)
Next
For k = 0 To mx(i, j)
'以下は、マクロの記録から学んだもの
Cells(15 + i, 2 + 10 * j + k).Select
With Selection.Interior
.Pattern = xlSolid
.PatternColorIndex = xlAutomatic
.ThemeColor = xlThemeColorAccent5
.TintAndShade = 0
.PatternTintAndShade = 0
End With
'以上は、マクロの記録から学んだもの
Next
For k = mx(i, j) + 1 To n - 1
'以下は、マクロの記録から学んだもの
Cells(15 + i, 2 + 10 * j + k).Select
With Selection.Interior
.Pattern = xlSolid
.PatternColorIndex = xlAutomatic
.ThemeColor = xlThemeColorAccent2
.TintAndShade = 0.399945066682943
.PatternTintAndShade = 0
End With
'以上は、マクロの記録から学んだもの
Next
Else
For k = 0 To n - 1
Cells(15 + i, 2 + 10 * j + k) = "*"
Next
End If
Next
Next
End Sub
Function kensyou(a() As Integer, n As Integer)
Dim b(81) As Byte, i As Integer, j As Integer
For i = 0 To n * n - 1
b(i) = 0
Next
For i = 0 To n - 1
For j = 0 To n - 1
b(a(i, j)) = 1
Next
Next
For i = 0 To n - 1
If b(i) = 0 Then
kensyou = 0
Exit Function
End If
Next
kensyou = 1
End Function
Private Sub CommandButton2_Click()
Rows("4:15").Select
Selection.ClearContents
Rows("15:35").Select
Selection.Delete
Range("A1").Select
End Sub
参考ダウンロード添付ファイル
多くの皆さんの頭には??????????????????????
が浮かび、頭が爆破しそうになっていると思います。
そこで、Sub sds(g As Integer) '数独作成プロシージャの解説を第8話と第9話で、
Sub klk(g As Integer) '局所リスト解析プロシージャの解説を第10話で行いたいと思います。
Rnd (-1)
Randomize Timer
が入っているために、同じ問題が出来る可能性は0.000000001%もありませんから、
ないと断言して良いでしょう。
ですから、何回ボタンを押しても下に例示する問題は出ません。
さて、
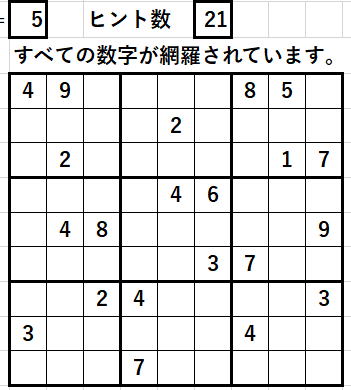
で一見数独の問題が出来たように思えますが、
例の条件
① 解答が存在する
② 別解が存在しない
の2つを満たしているかは、まだ確かめていません。
ヒント数が少ないので①は満たしているだろうと皆さんはお思いになるでしょうが、
実は、ヒント数21ぐらいで解のない問題が出来てしまう可能性は、
皆さんが予想するよりは高いのです。
①を満たしていたとしても②の条件の方は、もっと厳しいといえます。
以降の解説を読んで、理解しても数独自動生成ソフトの完成はまだまだ先の話なのです。
