第1話 互いに素
第30講の課題は、数字を
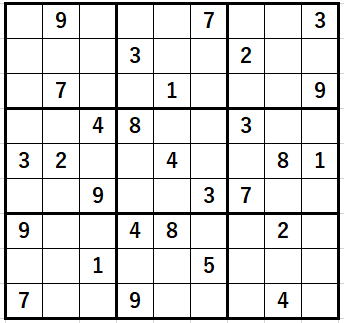
のように配置するにはどうしたらよいかを考えます。
ここでは、とりあえず数独(ナンプレ)のルールは無視して、数字の配置だけを考えます。
したがって、同じ行・列・ブロックに数字が重複しても気にしないということです。
数字の重複の改善は、第31講の局所リスト構造解析によって行います。
数独(ナンプレ)自動生成アプリ9×9・16×16・25×25統合版Ver.1(2017/03/16完成)
ではどのように配置しているかと申しますと、
互いに素という数学の考え方を用いています。
互いに素とは何か。
互いに素でない場合の例と互いに素である場合の例を挙げますので、
考えて下さい。
互いに素でない例
(4,6)、(12,18)、(27,51)
互いに素な例
(2,5)、(3,7)、(4,81)、(12,81)
答は例によって30行下です。
答
最大公約数が1の場合、2つの数字は互いに素といいます。
つまり、公約数が1しかない場合を互いに素というのです。
前の数字を分子に、後の数字を分母にして分数を作ったときに、
約分できない分数になる場合を互いに素であると説明することも出来ます。
(4,6)→4/6は約分できる
(2,5)→2/5は約分できない。
この互いに素である数字の組み合わせには、大変面白い性質があります。
(2,5)を例にしてみましょう。
はじめの数字は1以上5以下の任意の数字を取って、
1,2,3,4,5から2つ飛びに数字を選びます。
右がないときは一番左に戻るというルールにします。
例として、はじめの数字を3とします。
3→5→2→4→1
5回の操作で1から5までの数字がすべてそろいます。
はじめの数字を4としてみても、
4→1→3→5→2
どの数字ではじめても5回で必ずすべての数字を網羅できます。
では、互いに素でない場合はどうでしょうか。
(2,6)で例えばはじめの数字を3とすると、
3→5→1→3→5→1→・・・・
いつまでいっても、3→5→1の繰り返しで、
2,4,6は出てきません。
はじめの数字を4とすると、
4→6→2→4→6→2→・・・
今度は、1,3,5が落ちてしまいます。
(3,6)ならどうでしょうか。はじめの数字を3とすると、
3→6→3→6→・・・
何度今回は、3と6のみしか出てきません。
つまり、m<nで(m,n)が互いに素であるとき、
1からnまでの任意の数字からはじめて、
1からnの中からm個おきに数字をn回取っていくと、
1からnまでの数字が網羅されるという性質があるのです。
この性質を確認するために
参考ダウンロード添付ファイルを開いてVBAコードを入力して

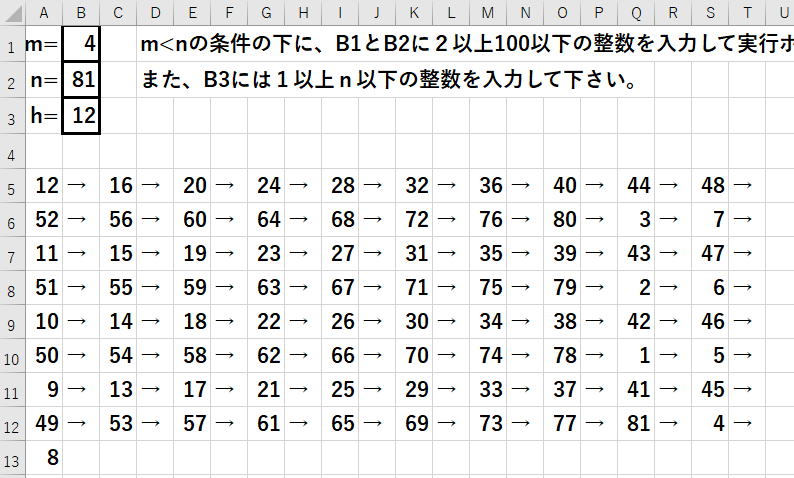
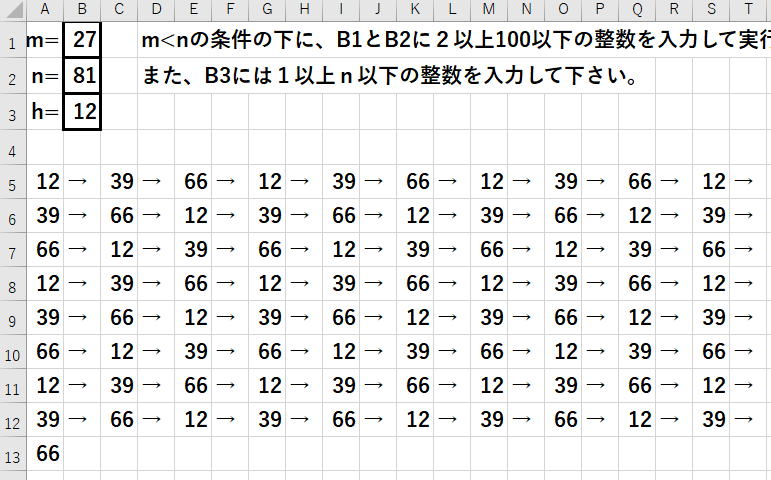
を実現できるプログラムを作って下さい。
hははじめの数です。
