第5話 全体構造解析を導入したプログラム例
Dim a(16, 16) As Byte, n As Byte, cn As Byte, ls(16, 16, 16) As Byte, m(16, 16) As Byte
Private Sub CommandButton1_Click()
CommandButton2_Click
cn = 0
n = 9
hj = Timer
Call sy
Call f(0) 'n次数独作成プロシージャ
Call h
ow = Timer
Cells(15, 13) = "問題を解くのにかかった時間は"
Cells(16, 13) = ow - hj
Cells(17, 13) = "秒です。"
End Sub
Sub sy()
Dim i As Byte, j As Byte, k As Byte, l As Byte, w As Byte
For i = 0 To 8
For j = 0 To 8
a(i, j) = 0
m(i, j) = 9
For k = 0 To 8
ls(i, j, k) = k + 1
Next
Next
Next
For i = 0 To 8
For j = 0 To 8
If Cells(4 + i, 3 + j) <> "" Then a(i, j) = Cells(4 + i, 3 + j)
Next
Next
For i = 0 To 8
For j = 0 To 8
If a(i, j) = 0 Then
For k = 0 To 8
If k <> j And a(i, k) > 0 Then
For l = 0 To 8
If ls(i, j, l) = a(i, k) Then
w = ls(i, j, m(i, j) - 1)
ls(i, j, m(i, j) - 1) = a(i, k)
ls(i, j, l) = w
m(i, j) = m(i, j) - 1
Exit For
End If
Next
End If
Next
For k = 0 To 8
If k <> i And a(k, j) > 0 Then
For l = 0 To m(i, j) - 1
If ls(i, j, l) = a(k, j) Then
w = ls(i, j, m(i, j) - 1)
ls(i, j, m(i, j) - 1) = a(k, j)
ls(i, j, l) = w
m(i, j) = m(i, j) - 1
Exit For
End If
Next
End If
Next
For k = 0 To 8
If i <> 3 * Int(i / 3) + Int(k / 3) And j <> 3 * Int(j / 3) + (k Mod 3) And a(3 * Int(i / 3) + Int(k / 3), 3 * Int(j / 3) + (k Mod 3)) > 0 Then
For l = 0 To m(i, j) - 1
If ls(i, j, l) = a(3 * Int(i / 3) + Int(k / 3), 3 * Int(j / 3) + (k Mod 3)) Then
w = ls(i, j, m(i, j) - 1)
ls(i, j, m(i, j) - 1) = a(3 * Int(i / 3) + Int(k / 3), 3 * Int(j / 3) + (k Mod 3))
ls(i, j, l) = w
m(i, j) = m(i, j) - 1
Exit For
End If
Next
End If
Next
End If
Next
Next
End Sub
Sub f(g As Byte)
If cn = 1 Then Exit Sub
Dim i As Byte, j As Byte, jy As Byte, jx As Byte, iii As Byte
Dim gy As Byte, gx As Byte
gy = Int(g / n)
gx = g Mod n
If a(gy, gx) > 0 Then
If g + 1 < n * n Then
Call f(g + 1)
Else
Call h
End If
Exit Sub
End If
For iii = 0 To m(gy, gx) - 1
i = ls(gy, gx, iii)
For j = 0 To 8
If j <> gx And a(gy, j) > 0 Then
If i = a(gy, j) Then GoTo tobi
End If
Next
For j = 0 To 8
If j <> gy And a(j, gx) > 0 Then
If i = a(j, gx) Then GoTo tobi
End If
Next
For j = gy - (gy Mod 3) To gy - (gy Mod 3) + 2
For k = gx - (gx Mod 3) To gx - (gx Mod 3) + 2
If (j <> gy And k <> gx) And (a(j, k) > 0) Then
If i = a(j, k) Then GoTo tobi
End If
Next
Next
a(gy, gx) = i
If g + 1 < n * n Then
Call f(g + 1)
If cn = 1 Then Exit Sub
Else
Call h
If cn = 1 Then Exit Sub
End If
tobi:
Next
a(gy, gx) = 0
End Sub
Sub h()
Dim i As Byte, j As Byte
For i = 0 To 8
For j = 0 To 8
Cells(15 + i, 3 + j) = a(i, j)
Next
Next
cn = cn + 1
End Sub
Private Sub CommandButton2_Click()
Rows("15:23").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル
実行結果
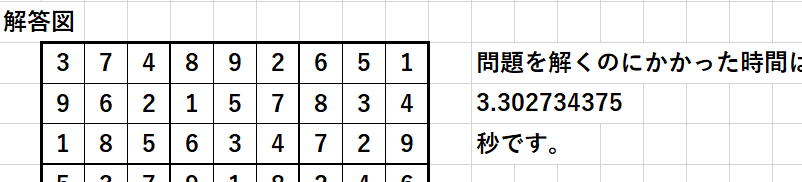
9.7秒から3.3秒へ躍進を遂げました。
さらに、すべて100未満の整数であることを考えて、
Integer型をすべてByte型に変更添付ファイル すると、
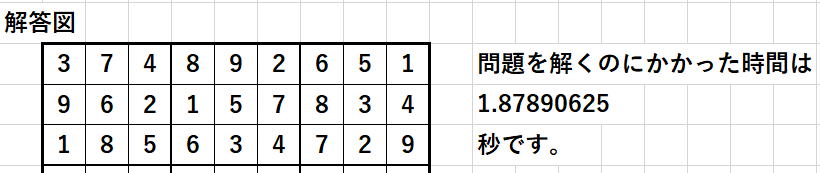
約2倍近くになります。最初のバージョンと比べると長足の進歩を遂げています。
実は、全体構造解析は、セルに値が入る度に変わります。
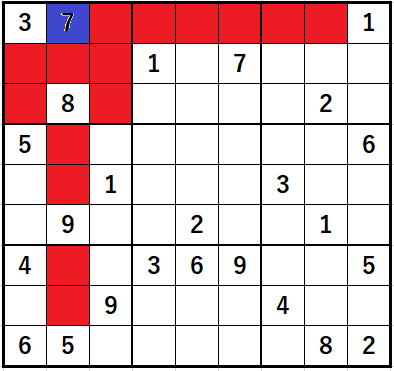
影響を受ける部分のみの解析する部分構造解析が必要になりますが、
これはかなり難しい課題ですので、
後の数独を扱う講で取り組みます。
この部分構造解析を取り入れると、
For iii = 0 To m(gy, gx) - 1
i = ls(gy, gx, iii)
For j = 0 To 8
If j <> gx And a(gy, j) > 0 Then
If i = a(gy, j) Then GoTo tobi
End If
Next
For j = 0 To 8
If j <> gy And a(j, gx) > 0 Then
If i = a(j, gx) Then GoTo tobi
End If
Next
For j = gy - (gy Mod 3) To gy - (gy Mod 3) + 2
For k = gx - (gx Mod 3) To gx - (gx Mod 3) + 2
If (j <> gy Or k <> gx) And (a(j, k) > 0) Then
If i = a(j, k) Then GoTo tobi
End If
Next
Next
a(gy, gx) = i
If g + 1 < n * n Then
Call f(g + 1)
If cn = 1 Then Exit Sub
Else
Call h
If cn = 1 Then Exit Sub
End If
tobi:
Next
の部分は
For i = 0 To m(gy, gx) - 1
a(gy, gx) = ls(gy, gx, i)
If g + 1 < n * n Then
Call f(g + 1)
If cn = 1 Then Exit Sub
Else
Call h
If cn = 1 Then Exit Sub
End If
tobi:
Next
と大変シンプルなものとなります。
入力の度に部分構造解析によって、
全体構造解析を修正していますので、
数独の禁則を犯す心配がないのです。
第3話と第5話のコードについて解説していませんので、
理解できずストレスがたまっている方が大勢いらっしゃると思います。
ごめんなさい。
次話以降で解説していきますので、
どうか諦めずに最後まで読んでください。
