第4話 全体構造解析の導入

問題をより速く解くためにまず導入したい工夫は、
セル構造解析です。
私がセル構造解析と呼んでいるものは、
そのセルに入る数字の候補数字と候補数字数を解析することです。
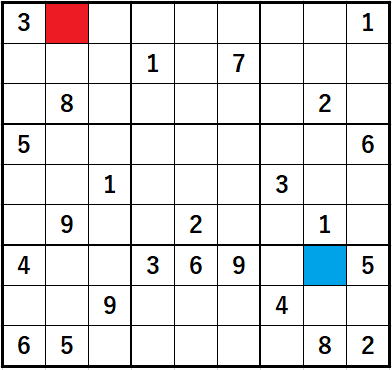
上の赤いセルの場合
まず、行(横列)の条件から、3と1が外されます。
次に列(縦列)の条件から8と9と5が外されます。
最後にブロックの条件から3と8が外されますが、
もうすでに行と列の条件から外されています。
結局赤のセルに入る候補数字は、
2,4,6,7
のみです。
候補数字数は4個です。
このような解析を全セルについて実行することを、
私は全体構造解析または問題構造解析と呼んでいます。
全体を入れている理由は、
さらに後ほど部分構造解析を導入するからです。
ですが、部分構造解析はとても難しい課題ですから、
これは独立した講になります。
全体構造解析をすることによって、
セルごとの候補数字が変わってきます。
Ver.1では全セルについて、
1,2,3,4,5,6,7,8,9
全部試していますが、

赤いセルは2,4,6,7のみを試せばよいですし、
水色のセルに至っては、7のみです。
(つまり、水色のセルは7に最初から確定しています。
仮定法を使わないで解ける数独は、
どの局面でも必ず確定できるセルが少なくとも1つは存在するのです。)
全体構造解析=全セル構造解析を行うために、
Dim ls(16, 16, 16) As Integer
という3次元グローバル配列を用意して、
(なぜ3次元になるかと申しますと、
赤いセルなら
ls(0, 1 ,0) = 2
ls(0, 1 ,1) = 4
ls(0, 1 ,2) = 6
ls(0, 1 ,3) = 7
がリストされます。
それぞれのセルごとに複数の候補数字がリストされますので、
3次元となるのです。
最初に2次元はセルの2次元に対応して、
3次元目は候補数字の順番(ただし、0から数える)に対応します。)
それぞれのセルのリスト(候補数字)を解析し、
さらに、
Dim m(16, 16) As Integer
2次元グローバル配列を用意して、そこに候補数字数を入力しておけば、
For i= 1 To n
For j = 0 To 8
If j <> gx And a(gy, j) > 0 Then
If i = a(gy, j) Then GoTo tobi
End If
Next
・・・・・
・・・・・
tobi:
Next
a(gy, gx) = 0
End Sub
(ランダムを外したバージョン)
の部分は、
For iii = 0 To m(gy, gx) - 1
i = ls(gy, gx, iii)
・・・・・
・・・・・
tobi:
Next
と変更することが出来ます。
では、皆さん
入力Subプロシージャgに全体構造解析を組み込んで下さい。
