第3話 数独を解くソフトVer.1の完成

を実現するプログラム例
Dim a(16, 16) As Integer, n As Integer, cn As Byte
Private Sub CommandButton1_Click()
CommandButton2_Click
cn = 0
n = 9
Randomize (Timer)
hj = Timer
Call sy
Call f(0) 'n次数独作成プロシージャ
Call h
ow = Timer
Cells(15, 13) = "問題を解くのにかかった時間は"
Cells(16, 13) = ow - hj
Cells(17, 13) = "秒です。"
End Sub
Sub sy()
Dim i As Integer, j As Integer
For i = 0 To 8
For j = 0 To 8
a(i, j) = 0
Next
Next
For i = 0 To 8
For j = 0 To 8
If Cells(4 + i, 3 + j) <> "" Then a(i, j) = Cells(4 + i, 3 + j)
Next
Next
End Sub
Sub f(g As Integer)
If cn = 1 Then Exit Sub
Dim i As Integer, j As Integer, jy As Integer, jx As Integer, ii As Integer, iii As Integer
Dim gy As Integer, gx As Integer
gy = Int(g / n)
gx = g Mod n
If a(gy, gx) > 0 Then
If g + 1 < n * n Then
Call f(g + 1)
Else
Call h
End If
Exit Sub
End If
ii = Int(10 * Rnd)
For iii = 1 To n
i = ((iii + ii) Mod 9) + 1
For j = 0 To 8
If j <> gx And a(gy, j) > 0 Then
If i = a(gy, j) Then GoTo tobi
End If
Next
For j = 0 To 8
If j <> gy And a(j, gx) > 0 Then
If i = a(j, gx) Then GoTo tobi
End If
Next
For j = gy - (gy Mod 3) To gy - (gy Mod 3) + 2
For k = gx - (gx Mod 3) To gx - (gx Mod 3) + 2
If (j <> gy And k <> gx) And (a(j, k) > 0) Then
If i = a(j, k) Then GoTo tobi
End If
Next
Next
a(gy, gx) = i
If g + 1 < n * n Then
Call f(g + 1)
If cn = 1 Then Exit Sub
Else
Call h
If cn = 1 Then Exit Sub
End If
tobi:
Next
a(gy, gx) = 0
End Sub
Sub h()
Dim i As Integer, j As Integer
For i = 0 To 8
For j = 0 To 8
Cells(15 + i, 3 + j) = a(i, j)
Next
Next
cn = cn + 1
End Sub
Private Sub CommandButton2_Click()
Rows("15:23").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル
難問が10秒程度で出来たので、
Ver.1としてはまあまあのできでといえるでしょうか。
しかし、私が作った最速のアプリなら、
この問題は0.00830078125秒で解けます。
ランダムが入れてあって、1回1回解く時間が違いますので、
ランダムを外したものも
参考ダウンロード添付ファイル
添付しておきます。
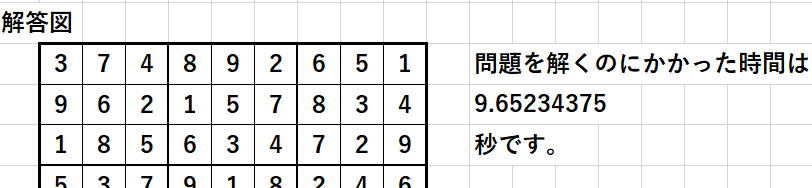
ランダムを外したバージョンは約9.7秒です。
改良を加えて最速に近づけていきます。
どのように改良したらよいか、次話で考えたいと思います。
