第３話 メルセンヌ数とメルセンヌ素数
メルセンヌ数とは、自然数ｎによって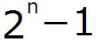
と表された数です。これを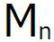
という記号で表します。メルセンに数を小さい順に並べますと、
１，３，７，１５，３１，６３，１２７，・・・
ということになります。
これは２進数で表したときの、
１，１１，１１１，１１１１，１１１１１，１１１１１，１１１１１１，・・・・
に対応します。
つまり、全部の位の数字が１からなる数字ということになります。
素数の性質は、何進数で表そうと同じですから、
もう一度１０進数に直します。
１，３，７，１５，３１，６３，１２７，・・・
この中で、３，７，３１はどういう数ですか。
そうです。
素数です。
どうしてメルセンヌ数が完全数の講に出てくるのでしょうか。
実は、メルセンヌ素数から完全数が作れるのです。
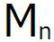が素数であるとき、
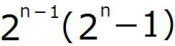が完全数になるのです。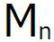が３であるとき、ｎ＝２ですね。このとき、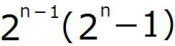
＝
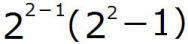＝２×３＝６です。
６＝１＋２＋３
で６は完全数です。
また、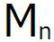
が７であるとき、ｎ＝３で、＝
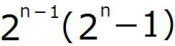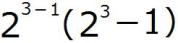＝４×７＝２８２８＝１＋２＋４＋７＋１４
で完全数です。
さらに、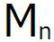
が３１であるとき、ｎ＝５で、＝
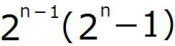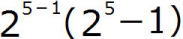＝１６×３１＝４６９これも完全数でしたね。
どうして、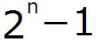
が素数のとき、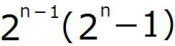が完全数になるのでしょうか。これは高校数学の範囲内で簡単に示すことが出来ます。
興味がある方は、新設されたページ素数と完全数の研究をご覧下さい。
では、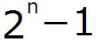
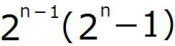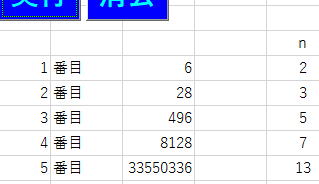
が素数のとき、は完全数であることを利用して、５番目までの完全数を求めるプログラムを考えて下さい。
