第2話 完全数4つの探索
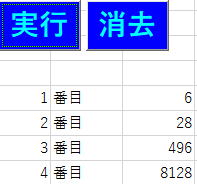
を実現するプログラム例
Private Sub CommandButton1_Click()
Dim i As Integer, cn As Byte
cn = 0
For i = 1 To 10000
If h(i) = 1 Then
cn = cn + 1
Cells(4 + cn, 1) = cn
Cells(4 + cn, 2) = "番目"
Cells(4 + cn, 3) = i
End If
Next
End Sub
Function h(i As Integer)
Dim a(1000) As Integer, b As Integer, j As Integer, cn As Integer, w As Integer
b = Int(i / 2)
cn = 0
For j = 1 To b
If i Mod j = 0 Then
a(cn) = j
cn = cn + 1
End If
Next
w = 0
For j = 0 To cn
w = w + a(j)
Next
If i = w Then h = 1 Else h = 0
End Function
Private Sub CommandButton2_Click()
Rows("5:2000").Select
Selection.ClearContents
Range("A1").Select
End Sub
参考ダウンロード添付ファイル
4つしか見つけられないのは、
情けないですが、
IntegerをLongに変更して
For i = 1 To 1000000
としても、見つかる完全数はやはり4つにすぎません。
5つ目は、33550336ですから、1万までで妥協しました。
5個目を見つけさせるには
For i = 1 To 3500000
としなければなりません。
実験してみましたが、かなり時間がかかりますので、
中止してしまいました。
Long型に変更しても8桁までしか探索できません。
C++なら、long long型がありますが、これとて19桁です。
ですから、366桁や770桁の完全数を見つけるには、
n進数演算の研究を続けるしかないわけです。
足し算、引き算の研究でさえ、
頭が爆発しそうになりましたよね。
かけ算はその2つより遙かに難しく、
割り算はかけ算よりずっと難しいのです。
でも、壁が厚く高いほど、やる気になりせんか。
770桁などの完全数の研究は、n進数研究に任せるにしても、
せめて5個目の8桁の33550336までは見つけたいと思いませんか。
完全数を見つける方法の1つとして、
メルセンヌ素数を利用する方法があります。
次話では、メルセンヌ素数について紹介します。
