第1話 完全数とは?
完全数は、古代ギリシャ以来いろいろな数学者が、
探索を続けてきたにもかかわらず、
まだ、49個しか見つかっていません。
コンピュータの性能が上がり、
スパコンが開発されている現在でも、
完全数の探索は困難を極めています。
最新から2番目に見つかった完全数は、
世界中の市民に、
空いているコンピュータの活用を求め、
見つけたといいます。
また、最新の発見は800台のコンピュータを連結して、
発見されたといいます。
その桁数は、約5千万桁だそうです。
私も一時完全数の探索に熱中したことがありますが、
私が見つけられた最大の完全数は770桁です。
50個目の完全数への登頂を試みましたが、
パソコン1台では、とても難しいことが分かり、
はかない夢と終わったのです。
実は、本講義ですでに2つの講で扱い、
この後も何回も戻る予定になっているn進数演算の研究は、
完全数の研究からもたらされたものです。
さて、完全数とは何でしょうか。
自分自身を除く約数の和が自分自身に一致する数です。
例を挙げると、
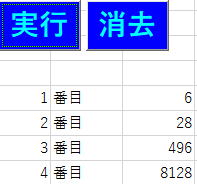
6=1+2+3
28=1+2+4+7+14
です。
次は、496ですが、これはギリシャ人が神とあがめた数ですし、
現代物理学最先端理論である超弦理論のキーワードにもなっているそうです。
素数と超弦理論の結びつきについては、前に述べたことがありますが、
超弦理論と完全数の間にも何か不思議な関係があるようです。
496の次は何だと思いますか。
8128です。
さらに、次は33550336と8桁になってしまいます。
そうです。
すぐに大きくなってしまうのです。
ですから、n進数演算が完成するまでは、
4個ぐらいの探索で妥協するしかないのです。
私が見つけた770桁の完全数でも15個目の完全数にすぎません。
さて、For文で1から1万ぐらいまでの整数を発生させて、
その中で完全数になっているものだけを列挙するプログラムを考えて下さい。