第4話 メルセンヌ素数を利用した完全数の5番目までの探索
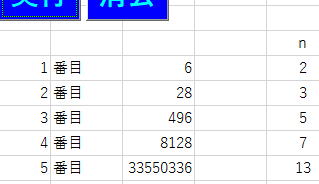
実現するプログラム例
Private Sub CommandButton1_Click()
Dim i As Integer, cn As Byte, w As Long
cn = 0
Cells(4, 5) = "n"
For i = 2 To 20
w = 1
For j = 1 To i
w = 2 * w
Next
w = w - 1
If sh(w) = 1 Then
For j = 1 To i - 1
w = 2 * w
Next
cn = cn + 1
Cells(4 + cn, 1) = cn
Cells(4 + cn, 2) = "番目"
Cells(4 + cn, 3) = w
Cells(4 + cn, 5) = i
If cn = 5 Then
Exit Sub
End If
End If
Next
End Sub
Function sh(w As Long)
Dim i As Long, a As Long
If w = 1 Then
sh = 0
Exit Function
End If
If w = 2 Then
sh = 1
Exit Function
End If
a = Sqr(w)
For i = 3 To a Step 2
If w Mod i = 0 Then
sh = 0
Exit Function
End If
Next
sh = 1
End Function
Private Sub CommandButton2_Click()
Rows("4:2000").Select
Selection.ClearContents
Range("A1").Select
End Sub
参考ダウンロード添付ファイル
このプログラムでも残念ながら、
5番目までの完全数しか探索できません。
If cn = 5 Then
Exit Sub
End If
を外すと残念ながらオーバーフローします。
つまり、今回の方法を使ったとしても8桁の完全数が限界です。
より、大きな完全数を見いだすためには、
n進数の研究を続けるしかありませんが、
そのときのために次話において、
が素数であるかどうかを判定する方法として、
リュカテストがあることを紹介しておきましょう。
n進数の研究を進めて
足し算・引き算に加えて
かけ算、割り算、平方根の計算まですすめて、
メルセンヌ数が素数であるかを判定できるようになっても、
求められる完全数の桁数は20桁もいきません。
20桁クラスのメルセンヌ数になると、
素数判定に大変時間がかかるからです。
しかし、
リュカテストを使うと効率的に素数判定ができるようになり、
770桁の完全数まで探索できるようになります。
