第5話 ユークリッド互除法を利用した分数約分判定と約分実行マクロ例


を実現するプログラム例
Private Sub CommandButton1_Click()
Rows("6:2000").Select
Selection.ClearContents
Cells(1, 1).Select
Dim a As Integer, b As Integer, c As Integer, d As Integer, e As Integer
a = f
b = f
c = a
d = b
Cells(4, 2) = c
Cells(5, 2) = d
If b > a Then Call g(a, b)
e = h(a, b)
If e > 1 Then
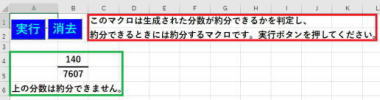
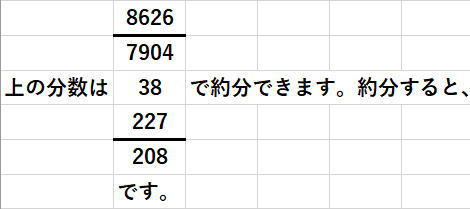
Cells(6, 1) = "上の分数は"
Cells(6, 2) = e
Cells(6, 3) = "で約分できます。約分すると、"
Cells(7, 2) = Int(c / e)
Cells(8, 2) = Int(d / e)
Cells(9, 2) = "です。"
Else
Cells(6, 1) = "上の分数は約分できません。"
End If
End Sub
Function f()
tobi:
f = Int(10000 * Rnd)
If f = 0 Then GoTo tobi
End Function
Sub g(a As Integer, b As Integer)
Dim w As Integer
w = a
a = b
b = w
End Sub
Function h(a As Integer, b As Integer)
a = a Mod b
If a = 0 Then
h = b
Exit Function
End If
h = h(b, a)
End Function
Private Sub CommandButton2_Click()
Rows("4:2000").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル
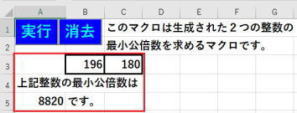
ユークリッド互除法を使うと、最小公倍数を求めることも出来ます。
aとbの最大公約数をG、最小公倍数をLとすると、
G×L=a×b
の関係があります。
ですから、最小公倍数Lを求めるには、
L=a×b÷G
ということになります。
最小公倍数を求めるプログラムを以下の条件下で組んで下さい。
① 整数a、bは今回の約分プログラムと同様にランダムに発生させる。
② 任意に発生させるだけだと、
ほとんどの場合互いに素(最大公約数が1)になってしまうので、
aもbも20未満の整数を3つかけたものとする。

※ L=a×b÷Gだと、a×bの部分がInteger型であるとオーバーフローしますから、
工夫して下さい。
