第9話 列の3on3解析を行うFunctionプロシージャコード例
Function tonty(g As Byte, ys() As Byte, t As Byte, ny As Byte) '列についての3on3解析を行うFunctionプロシージャ
'引数のnyは、内容(naiyou)の略、呼び出し側のライン排除確定プロシージャのiに当たる。
'i + 1は、数独配列p(○, ○)に入力する内容(1から9の値)であった。
'確定法で解く=仮定法を使わないので復元規定は最初から記述しない。
Dim i As Byte, j As Byte, k As Byte, l As Byte, m As Byte, o As Byte, w As Byte
Dim ys1(8) As Byte 'y座標を記録する変数
Dim ys2(8) As Byte 'y座標を記録する変数
tonty = 1
Dim xs1(8) As Byte 'x座標を記録する変数
Dim xs2(8) As Byte 'x座標を記録する変数
tonty = 1
For i = ny + 1 To n_1
'i + 1 は数独配列p(○, ○)に入れる2番目の内容(1から9の値)
'もっと正確に説明すると、3on3のセルにおけるリストの2番目となる可能性のある値である。
'可能性という言い方をしたのは、以下の条件を満たしてはじめて2番目のリストになるから。
w = 0
For j = 0 To n_1 'jはx座標(横座標)
If p(j, t) = 0 Then 's = ys(0)
If kh(j, t, i) = 1 Then
ys1(w) = j
w = w + 1
End If
End If
Next
If w = 3 Then
If ys(0) = ys1(0) And ys(1) = ys1(1) And ys(2) = ys1(2) Then
For j = 0 To n_1 'j + 1 は3on3セルの3番目のリスト候補
If j <> ny And j <> i Then
w = 0
For k = 0 To n_1 'kはx座標(横座標)
If p(k, t) = 0 Then 's = ys(0)
If kh(k, t, j) = 1 Then
ys2(w) = k
w = w + 1
End If
End If
Next
If w = 2 Or w = 3 Then
If (ys2(0) = ys(0) And ys2(1) = ys(1)) Or (ys2(0) = ys(0) And ys2(2) = ys(2)) Or (ys2(1) = ys(1) And ys2(2) = ys(2)) Then
'以降3on3確定による破綻処理
For k = 0 To n_1
If k <> ys(0) And k <> ys(1) And k <> ys(2) Then
If p(k, t) = 0 Then
If mx(k, t) = 2 Then
w = 0
For l = 0 To 2
If rlst(k, t, l) = ny + 1 Or rlst(k, t, l) = i + 1 Or rlst(k, t, l) = j + 1 Then
w = w + 1
End If
Next
If w = 3 Then
tonty = 0
Exit Function
End If
End If
If mx(k, t) = 1 Then
w = 0
For l = 0 To 1
If rlst(k, t, l) = ny + 1 Or rlst(k, t, l) = i + 1 Or rlst(k, t, l) = j + 1 Then
w = w + 1
End If
Next
If w = 2 Then
tonty = 0
Exit Function
End If
End If
If mx(k, t) = 0 Then
If rlst(k, t, 0) = ny + 1 Or rlst(k, t, 0) = i + 1 Or rlst(k, t, 0) = j + 1 Then
tonty = 0
Exit Function
End If
End If
End If
End If
Next
'3on3確定による破綻処理終了
' Cells(4 + Int(cnt / 50), 1 + (cnt Mod 50)) = "X"
' cnt = cnt + 1
'以降3on3確定による排除解析
For k = 0 To n_1
If k <> ys(0) And k <> ys(1) And k <> ys(2) Then
If p(k, t) = 0 Then
For l = 0 To mx(k, t)
If ny + 1 = rlst(k, t, l) Then
rlst(k, t, l) = rlst(k, t, mx(k, t))
rlst(k, t, mx(k, t)) = ny + 1
kh(k, t, ny) = 0
mx(k, t) = mx(k, t) - 1
Exit For
End If
Next
For l = 0 To mx(k, t)
If i + 1 = rlst(k, t, l) Then
rlst(k, t, l) = rlst(k, t, mx(k, t))
rlst(k, t, mx(k, t)) = i + 1
kh(k, t, i) = 0
mx(k, t) = mx(k, t) - 1
Exit For
End If
Next
For l = 0 To mx(k, t)
If j + 1 = rlst(k, t, l) Then
rlst(k, t, l) = rlst(k, t, mx(k, t))
rlst(k, t, mx(k, t)) = j + 1
kh(k, t, j) = 0
mx(k, t) = mx(k, t) - 1
Exit For
End If
Next
End If
End If
Next
'3on3確定による排除解析終了
'以降3on3確定解析
Dim kr(2) As Byte
For k = 0 To 2
kr(k) = 0
Next
w = 0
For k = 0 To mx(ys(0), t)
If ny + 1 = rlst(ys(0), t, k) Then
kr(0) = 1
w = w + 1
Exit For
End If
Next
For k = 0 To mx(ys(0), t)
If i + 1 = rlst(ys(0), t, k) Then
kr(1) = 1
w = w + 1
Exit For
End If
Next
For k = 0 To mx(ys(0), t)
If j + 1 = rlst(ys(0), t, k) Then
kr(2) = 1
w = w + 1
Exit For
End If
Next
If w = 3 Then
rlst(ys(0), t, 0) = ny + 1
rlst(ys(0), t, 1) = i + 1
rlst(ys(0), t, 2) = j + 1
mx(ys(0), t) = 2
End If
If w = 2 Then
w = 0
If kr(0) = 1 Then
rlst(ys(0), t, w) = ny + 1
w = w + 1
End If
If kr(1) = 1 Then
rlst(ys(0), t, w) = i + 1
w = w + 1
End If
If kr(2) = 1 Then
rlst(ys(0), t, w) = j + 1
w = w + 1
End If
mx(ys(0), t) = 1
End If
For k = 0 To 2
kr(k) = 0
Next
w = 0
For k = 0 To mx(ys(1), t)
If ny + 1 = rlst(ys(1), t, k) Then
kr(0) = 1
w = w + 1
Exit For
End If
Next
For k = 0 To mx(ys(1), t)
If i + 1 = rlst(ys(1), t, k) Then
kr(1) = 1
w = w + 1
Exit For
End If
Next
For k = 0 To mx(ys(1), t)
If j + 1 = rlst(ys(1), t, k) Then
kr(2) = 1
w = w + 1
Exit For
End If
Next
If w = 3 Then
rlst(ys(1), t, 0) = ny + 1
rlst(ys(1), t, 1) = i + 1
rlst(ys(1), t, 2) = j + 1
mx(ys(1), t) = 2
End If
If w = 2 Then
w = 0
If kr(0) = 1 Then
rlst(ys(1), t, w) = ny + 1
w = w + 1
End If
If kr(1) = 1 Then
rlst(ys(1), t, w) = i + 1
w = w + 1
End If
If kr(2) = 1 Then
rlst(ys(1), t, w) = j + 1
w = w + 1
End If
mx(ys(1), t) = 1
End If
For k = 0 To 2
kr(k) = 0
Next
w = 0
For k = 0 To mx(ys(2), t)
If ny + 1 = rlst(ys(2), t, k) Then
kr(0) = 1
w = w + 1
Exit For
End If
Next
For k = 0 To mx(ys(2), t)
If i + 1 = rlst(ys(2), t, k) Then
kr(1) = 1
w = w + 1
Exit For
End If
Next
For k = 0 To mx(ys(2), t)
If j + 1 = rlst(ys(2), t, k) Then
kr(2) = 1
w = w + 1
Exit For
End If
Next
If w = 3 Then
rlst(ys(2), t, 0) = ny + 1
rlst(ys(2), t, 1) = i + 1
rlst(ys(2), t, 2) = j + 1
mx(ys(2), t) = 2
End If
If w = 2 Then
w = 0
If kr(0) = 1 Then
rlst(ys(2), t, w) = ny + 1
w = w + 1
End If
If kr(1) = 1 Then
rlst(ys(2), t, w) = i + 1
w = w + 1
End If
If kr(2) = 1 Then
rlst(ys(2), t, w) = j + 1
w = w + 1
End If
mx(ys(2), t) = 1
End If
'3on3確定解析終了
Exit For
End If
End If
End If
Next
End If
End If
Next
End Function
テキスト形式の添付ファイル
さて、次はブロックの3on3解析を行うFunctionプロシージャ
tontxのコードをコピペして、
編集の置換において、
カレント プロシージャ内で「すべて置換」するを使って効率的に、
コーティングしてくださいという点は同じですが、
列より、いくつか難しい点があります。
注意深く置換していって、
もし失敗してしまった場合にはあわてずに、
Ctrl+Zを使い、1つ手前あるいは必要な段階まで戻れば大丈夫ですよ。
念のために「名前を変えて保存」するでバックアップをとっておくと尚いいかと思います。
バックアップファイル名は、
例えば「数独作成アプリVer4-4-25-5-35」
のようにすると良いかも知れません。
4-25-5-35は4月25日5時35分です。
このようにしておくと、どれが最新バージョンなのか分かります。
もちろん、バックアップファイルはたくさん出来てしまいますが、
ハードディスクの無駄使いであると思えば、
完成した時点で本体今の場合は、
「数独作成アプリVer4」以外のファイルをすべて削除すれば、
メモリ容量の無駄遣いにはなりません。
エクセルファイルですからたいした容量ではありませんから、
私は、基本的にはファイルの削除はしません。
エクセルファイルごときで、
ハードディスクの容量を圧迫することなど考えられないからです。
尚、ブロックの2on2解析すなわち相補確定解析に一部誤りがありました。
これを機会に訂正しておきます。
その訂正点も踏まえて、
ブロックの3on3解析Functionプロシージャtontbをコーティングして下さい。
If (xbs + la <> xs(0) And ybs + ls <> ys(0)) And (xbs + la <> xs(1) And ybs + ls <> ys(1)) Then
という記述が2カ所ありますが、
If (xbs + la <> xs(0) Or ybs + ls <> ys(0)) And (xbs + la <> xs(1) Or ybs + ls <> ys(1)) Then
が正解です。
もし、局所リスト構造解析においては
If (xbs + la <> xs(0) And ybs + ls <> ys(0)) Then
でよいのですが、相補確定解析や3on3解析ではOrとしなければなりません。
局所リスト構造解析の場合にAndとしたのは、Orだと

(青のセルが(xbs + la <> xs(0)))
該当セル(xbs + la <> xs(0))以外がすべて解析対象になってしまいます。
ですが、これは無駄があります。
なぜなら、ブロックの解析がなされる前に、
行と列の解析が行われ、

緑の部分については解析積みですから、
解析が重複するわけです。
Andに変更すると、
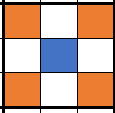
濃いオレンジのみが解析対象になり無駄をなくすることが出来ます。
しかし、1:1対応解析の場合
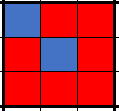
赤がすべて解析対象ですが、 Andにしてしまうと、

黄色のセルのみが改正対象になり、

紫が解析対象から外されてしまい、
正しい解析が出来なくってしまいます。
ですから、Orでなければならないのです。
今回は、基本10話以内にするという私の方針は守れません。
まだ、いくつか説明しなければならない点があるからです。
