Dim rh(80) As Byte
Private Sub CommandButton1_Click()
・
Sub sds(g As Byte, mok As Byte) '数独作成プロシージャ
If mok = 0 Then If cn = 1 Then Exit Sub
・
If u = 1 Then '局所リスト解析プロシージャ
If g + 1 < n2 Then
Call nck(g + 1, mok)
Call sds(g + 1, mok)
If rh(g + 1) = 1 Then
mx(y(g + 1), x(g + 1)) = cmx(g + 1, y(g + 1), x(g + 1))
For j = 0 To n_1
rlst(y(g + 1), x(g + 1), j) = crlst(g + 1, y(g + 1), x(g + 1), j)
Next
For j = 0 To n_1
kh(y(g + 1), x(g + 1), j) = ckh(g + 1, y(g + 1), x(g + 1), j)
Next
End If
・
End Sub
Sub rhk(g As Byte) 'ライン排除確定解析プロシージャ
Dim i As Byte, j As Byte, k As Byte, l As Byte, w As Byte 'wは行・列・ブロックにおける白の個数を数えるカウンタ
Dim ys As Byte 'y座標を記録する変数
Dim xs As Byte 'x座標を記録する変数
rh(g) = 0
'以下各数字に対応する行におけるライン排除確定があるかを調べるための手順
For i = 0 To n_1 'i + 1 は入力する数字を示す。
For j = 0 To n_1 'jはy座標(縦座標)
'以下行における白のセルのカウント
w = 0
For k = 0 To n_1 'kはx座標(横座標)
If p(j, k) = 0 Then
If kh(j, k, i) = 1 Then
xs = k
w = w + 1
End If
End If
Next
If w = 1 Then
For k = 0 To mx(j, xs)
If rlst(j, xs, k) = i + 1 Then
y(g) = j
x(g) = xs
cmx(g, y(g), x(g)) = mx(y(g), x(g))
For l = 0 To n_1
crlst(g, y(g), x(g), l) = rlst(y(g), x(g), l)
Next
For l = 0 To n_1
ckh(g, y(g), x(g), l) = kh(y(g), x(g), l)
Next
rlst(y(g), x(g), k) = rlst(y(g), x(g), 0)
rlst(y(g), x(g), 0) = i + 1
mx(y(g), x(g)) = 0
rh(g) = 1
Exit Sub
End If
Next
End If
'以上行における白いセルのカウント
Next
Next
' 以下各数字に対応する列におけるライン排除確定があるかを調べるための手順
For i = 0 To n_1 'i + 1 は入力する数字を示す。
For j = 0 To n_1 'jはy座標(縦座標)
'以下行における白のセルのカウント
w = 0
For k = 0 To n_1 'kはx座標(横座標)
If p(k, j) = 0 Then
If kh(k, j, i) = 1 Then
ys = k
w = w + 1
End If
End If
Next
If w = 1 Then
For k = 0 To mx(ys, j)
If rlst(ys, j, k) = i + 1 Then
y(g) = ys
x(g) = j
cmx(g, y(g), x(g)) = mx(y(g), x(g))
For l = 0 To n_1
crlst(g, y(g), x(g), l) = rlst(y(g), x(g), l)
Next
For l = 0 To n_1
ckh(g, y(g), x(g), l) = kh(y(g), x(g), l)
Next
rlst(y(g), x(g), k) = rlst(y(g), x(g), 0)
rlst(y(g), x(g), 0) = i + 1
mx(y(g), x(g)) = 0
rh(g) = 1
Exit Sub
End If
Next
End If
'以上行における白いセルのカウント
Next
Next
'以下各数字に対応するブロックにおけるライン排除確定があるかを調べるための手順
Dim ybs As Byte, xbs As Byte
Dim ks As Byte, ka As Byte
For i = 0 To n_1 'i + 1 は入力する数字を示す。
For j = 0 To n_1 'jはy座標(縦座標)
ybs = rn * Int(j / rn)
xbs = rn * (j Mod rn)
'以下行における白のセルのカウント
w = 0
For k = 0 To n_1 'kはx座標(横座標)
ks = Int(k / rn)
ka = k Mod rn
If p(ybs + ks, xbs + ka) = 0 Then
If kh(ybs + ks, xbs + ka, i) = 1 Then
ys = ybs + ks
xs = xbs + ka
w = w + 1
End If
End If
Next
If w = 1 Then
For k = 0 To mx(ys, xs)
If rlst(ys, xs, k) = i + 1 Then
y(g) = ys
x(g) = xs
cmx(g, y(g), x(g)) = mx(y(g), x(g))
For l = 0 To n_1
crlst(g, y(g), x(g), l) = rlst(y(g), x(g), l)
Next
For l = 0 To n_1
ckh(g, y(g), x(g), l) = kh(y(g), x(g), l)
Next
rlst(y(g), x(g), k) = rlst(y(g), x(g), 0)
rlst(y(g), x(g), 0) = i + 1
mx(y(g), x(g)) = 0
rh(g) = 1
Exit Sub
End If
Next
End If
'以上行における白いセルのカウント
Next
Next
End Sub
Sub nck(g As Byte, mok As Byte)
Dim i As Byte, j As Byte, mn As Byte, ik As Byte, jk As Byte
mn = 100
For i = 0 To n_1
For j = 0 To n_1
If p(i, j) = 0 Then
If mn > mx(i, j) Then
mn = mx(i, j)
ik = i
jk = j
If mn = 0 Then
y(g) = ik
x(g) = jk
Exit Sub
End If
End If
End If
Next
Next
y(g) = ik
x(g) = jk
If mok = 1 Then
rhk (g)
End If
End Sub
・
数独作成アプリVer.2一歩前バージョン
Ver.2によって1200題を作成するソフト
と前話の1200題適正検証ソフト
によってすべて○になることを確認して下さい。
30題に1題の割合で、
別解のある問題を作ってしまうという不具合の問題の解消に丸2日もかかってしまいました。
基本的には、復元プロシージャhukubenと同様に、
変更したセルの場所を時間を含む配列hth(g, i, j)に記録して、
変更したセルを元に戻すという方式で、
いいはずなのですが、
どうしてもこの配列を使う方法では成功しませんでした。
で、結局
Dim rh(80) As Byte
を導入して、不具合を解消できました。
第6話でも述べましたように、
今の方式は、
今回1つでも確定できるセルが見つかった段階で、
強制的にライン排除確定解析プロシージャSub rhk(g As Byte) を抜けるようになっていますので、
変更される場所は1カ所のみですから、
3次元配列にする必要はないというのはわかりますが、
hth(g, i, j)を使ってはいけないということはないと思いますで、
If hth(g + 1, y(g + 1), x(g + 1)) = 1 Then
mx(y(g + 1), x(g + 1)) = cmx(g + 1, y(g + 1), x(g + 1))
For j = 0 To n_1
rlst(y(g + 1), x(g + 1), j) = crlst(g + 1, y(g + 1), x(g + 1), j)
Next
For j = 0 To n_1
kh(y(g + 1), x(g + 1), j) = ckh(g + 1, y(g + 1), x(g + 1), j)
Next
End If
で何が問題なのかは、今も分かりません。
さて、第6講最後の課題です。
今回、ライン排除確定を組み込みましたが、
最後に破綻処理を入れて
数独作成アプリVer.2の完成としましょう。
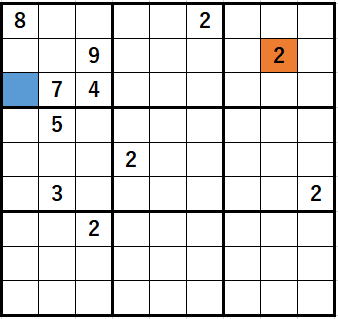
オレンジのセルに2を入れると、
ライン排除確定によって、
青のセルが2に確定しますが、
この確定によって破綻しています。
何故かというと、
確定によって新たな排除が発生して、
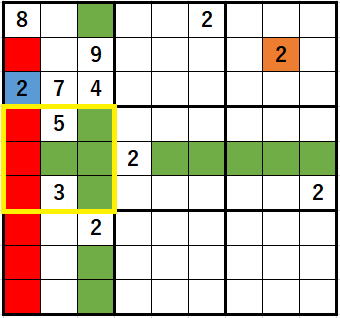
黄色の囲いのブロックに2を入れる場所がなくなってしまいます。
数独作成アプリVer.2一歩前バージョン
はライン排除確定のみを組み込んだだけで、
ライン排除確定による排除を組み込んでいませんので、
破綻判定が出来ずに、
無駄に試行錯誤が繰り返される可能性があります。
そこで、ライン排除確定による排除を組み込みこむことによって、
オレンジのセルに2を入れると破綻することをプログラムに教えてやって下さい。
Sub rhkとSub nckはFunctionプロシージャに変更する必要があると思います。
