第3話 全体リスト構造解析Total方式の解説その1
tk '全体リスト構造解析Total方式
のコード
Sub tk()
Dim i As Byte, j As Byte, k As Byte, l As Byte, w As Byte
Dim kh(8, 8, 8) As Byte
For i = 0 To n_1
For j = 0 To n_1
ccmx(i, j) = 0
For k = 0 To n_1
ccrlst(i, j, k) = 0
kh(i, j, k) = 1 '1が白
Next
Next
Next
For i = 0 To n_1
For j = 0 To n_1
If p(i, j) = 0 Then
For k = 0 To n_1
If p(i, k) > 0 Then
kh(i, j, p(i, k) - 1) = 0
End If
Next
End If
Next
Next
For i = 0 To n_1
For j = 0 To n_1
If p(j, i) = 0 Then
For k = 0 To n_1
If p(k, i) > 0 Then
kh(j, i, p(k, i) - 1) = 0
End If
Next
End If
Next
Next
Dim ybs As Byte, xbs As Byte
Dim js As Byte, ja As Byte
Dim ks As Byte, ka As Byte
For i = 0 To n_1
ybs = rn * Int(i / rn)
xbs = rn * (i Mod rn)
For j = 0 To n_1
js = Int(j / rn)
ja = j Mod rn
If p(ybs + js, xbs + ja) = 0 Then
For k = 0 To n_1
ks = Int(k / rn)
ka = k Mod rn
If k <> j And p(ybs + ks, xbs + ka) > 0 Then
kh(ybs + js, xbs + ja, p(ybs + ks, xbs + ka) - 1) = 0
End If
Next
End If
Next
Next
For i = 0 To n_1
For j = 0 To n_1
If p(i, j) = 0 Then
w = 0
For k = 0 To n_1
If kh(i, j, k) = 1 Then
ccrlst(i, j, w) = k + 1
ccmx(i, j) = ccmx(i, j) + 1
w = w + 1
End If
Next
End If
Next
Next
' hyouji4
End Sub
この方式は、私が数独問題解法ソフトを一番最初に開発したときの方式です。
この方式は数独の問題を解くプログラムVer8等にも引き継がれています。
Dim kh(8, 8, 8) As Byteは何の配列かと申しますと、
kh(4, 5, 7) = 0 ならば、セル(4,5)には8(=7+1)が入力可能ですし、
kh(4, 5, 7) = 1 ならば、セル(4,5)には8(=7+1)が入力不可であること意味します。
注釈文には1が黒で、0が白と書いてありますが、
実際には1の方は9色の色があるとイメージして下さい。
例えば、1が次のように配置されていれば、
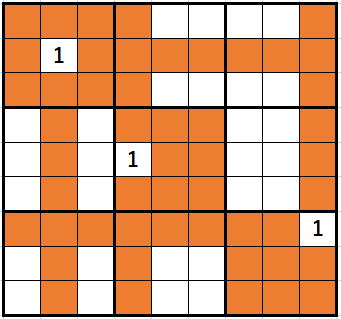
オレンジのところには、1は入力不可です。
同様に2についても、
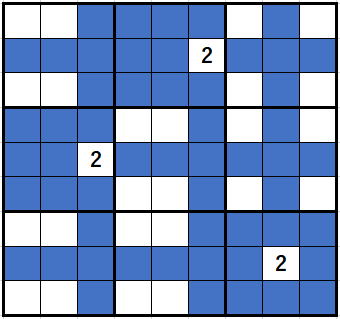
青色には2が入力不可です。
このような配置図を1から9まで行うので、
黒ではなく9色であるとイメージした方が良いのです。
For i = 0 To n_1
For j = 0 To n_1
ccmx(i, j) = 0
For k = 0 To n_1
ccrlst(i, j, k) = 0
kh(i, j, k) = 1 '1が白
Next
Next
Next
によって、kh(i, j, k) は最初すべて白に初期化されます。
ccrlst(i, j, k)がrlst(i, j, k)に対応しますが、
こちらでは0に初期化されています。
ですので、リスト構造解析を行ったときには、
対象外は0となります。
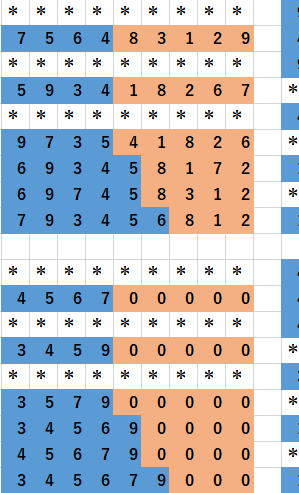
上が今開発中の数独作成ソフトによる全体リスト構造解析であるのに対して、
下がTotal方式の全体リスト構造解析です。
Total方式では、復元するときに困るのでは?
その問に対する答は、復元はしないです。
問題の分析のときにのみ、この全体構造解析を行います。
問題ですから、問題に配置されている数字はいじってはいけないわけです。
セルの数字を入れ直すときに復元の必要性が生じるのですが、
問題のセルの数字はいじってはいけないのですから、
復元の必要がないのです。
もちろん解答を作る際の試行錯誤においては、
最初の有効範囲(ブルー)内での数独作成アプリVer.1のような、
順番の変更と色替えが行われるわけです。
