第10話 Ver.2のコード解説その3
コード主要部分再掲
For k = 0 To 8
If k <> j And a(i, k) > 0 Then
For l = 0 To 8
If ls(i, j, l) = a(i, k) Then
w = ls(i, j, m(i, j) - 1)
ls(i, j, m(i, j) - 1) = a(i, k)
ls(i, j, l) = w
m(i, j) = m(i, j) - 1
Exit For
End If
Next
End If
Next
この部分は、前話の解説でお分かりのように、
水色の部分を動いていました。では、
For l = 0 To 8
If ls(i, j, l) = a(i, k) Then
w = ls(i, j, m(i, j) - 1)
ls(i, j, m(i, j) - 1) = a(i, k)
ls(i, j, l) = w
m(i, j) = m(i, j) - 1
Exit For
End If
Next
においては、何をしているのでしょうか。
k = 0 のときを例に説明しましょう。
これは図の
3の場合です。
ずばり、オレンジの任務は
『3をリストから外す!』
です。
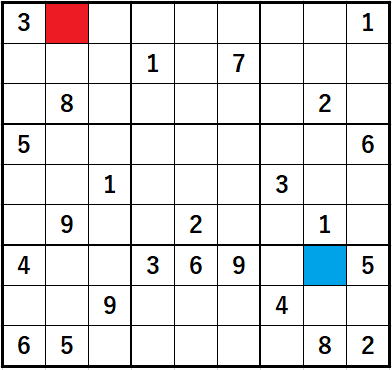
初期化によって、赤色のセルのリスト(候補数字)は
1,2,3,4,5,6,7,8,9
で、候補数字数も9個にされていました。
k = 0の場合、
オレンジが実行されると、
1,2,9,4,5,6,7,8,3
となり、候補数字数も8個になります。
つまり、有効リストは
1,2,9,4,5,6,7,8,3
となります。候補数字数が8個ということは、
最初の8個が実際に使われるリスト(候補数字)だということです。
(実際に使われるリストを有効リストと表現したわけです。)
つまり、3は対象外にされるということです。
1,2,9,4,5,6,7,8,*
ただし、今回開発したソフトは試行錯誤(トライ&エラー)によって問題を解いていますから、
失敗してしまった場合復元しなければなりませんので、
1,2,9,4,5,6,7,8,3
3をリストから1時的に外しているだけです。
今回開発したソフトは、実は常に9個がリストされています。
どこまでが有効かがm(i, j)によって示されているわけです。
m(i, j) = m(i, j) - 1の操作によって、最大リスト数m(i, j)は、
9個から8個にされるわけです。
For l = 0 To 8
If ls(i, j, l) = a(i, k) Then
w = ls(i, j, m(i, j) - 1)
ls(i, j, m(i, j) - 1) = a(i, k)
ls(i, j, l) = w
m(i, j) = m(i, j) - 1
Exit For
End If
Next
では、緑の枠割りは何でしょうか。
3と9の交換です。

プログラムの一番最初においては、赤いセルのリスト順は、
1,2,3,4,5,6,7,8,9
となっていますが、
プログラムが進むと、リストの順番はどんどん変更されていて、
7,8,4,5,1,3,6,9,2
等となっていたりします。
そうすると、外したい数字がどこにあるか分からないわけです。
外したい数字が何番目にリストされているのかを探す仕事をしているのが、
For l = 0 To 8
If ls(i, j, l) = a(i, k) Then
の部分です。これが分かれば、次の3行に任務は明らかです。
w = ls(i, j, m(i, j) - 1)
ls(i, j, m(i, j) - 1) = a(i, k)
ls(i, j, l) = w
そうです。
m(i, j)が9で、リスト順が
1,2,3,4,5,6,7,8,9
ならば、3と9の交換ですし、
m(i, j)が7で、リスト順が
7,8,4,5,1,3,6,9,2
ならば、3と6の交換です。
3と6を交換
7,8,4,5,1,6,3,9,2
してから、m(i, j) = m(i, j) - 1によって有効範囲を1つ減らして、
7,8,4,5,1,6,3,9,2
としているわけです。
Exit For
については、何も説明は必要ないですね。
外す候補数字が分かれば、
For文によるそれ以上の探索は無意味ですから、
強制的にFor文を終了させているわけです。
一応Ver.2の解説は一通り終わりました。
解説されても『全然分からない!!!!』の感想をお持ちの方がたくさんいらっしゃるでしょう。
でも、忍耐強く何回も読み返して下さい。
そして、5,6回読んで分からなかったとしても悲観なさらないで下さい。
少し時間をおいてから読み返すと電撃にあったように理解できたり、
自分でプログラミングしていくと分かったりするものです。
対象が難しいのですから、
簡単に理解できなくて当然です。
数独=ナンプレはルールは簡単ですが、
かなり奥が深いわけです。
ですから、世界選手権が開かれるほど人気があるわけです。
良問難問数独自動生成アプリVer.4(対称形) 数独自動生成(初心者から中級者用)アプリ
等を開発した私ですが、
数独の奥義は、まだまだ理解していないような気がしています。
ですから、皆さんあきらめないで粘り強く取り組んで下さい。
これで第23講は終了して、第24講では各種のグラフに挑戦します。
グラフを作るのは、C言語、C++、Java等では特別の技術が必要ですが、
幸いにしまして、エクセルにはグラフを簡単に作成できる機能があります。
これを利用してVBAでいろいろなグラフを作成してみましょう。
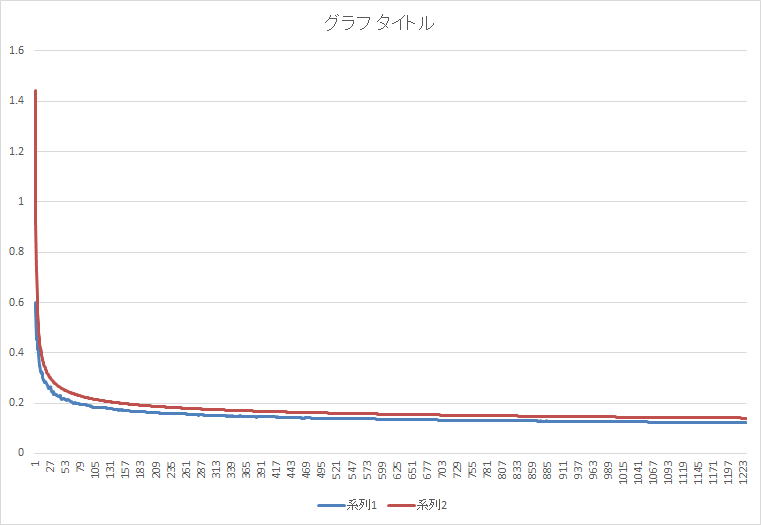
(素数の実際の存在確率−系列1とガウスの近似式による存在確率-系列2)
