第8話 シード値による乱数系列の指定
最適シード値探索プログラム例
Dim a(10, 10) As Byte, n As Byte, cn As Long, y(100) As Byte, x(100) As Byte
Dim hj As Variant, ow As Variant, Min As Variant
Private Sub CommandButton1_Click()
Min = 50
For i = 0 To 99
CommandButton2_Click
hj = Timer
cn = 0
n = Cells(4, 2)
Rnd (-1)
Randomize (i)
Call zy
Call f(0) 'n次魔方陣作成プロシージャ
ow = Timer
Cells(4, 16) = "生成にかかった時間は"
Cells(4, 20) = ow - hj
Cells(4, 21) = "秒です。"
If Min > ow - hj Then
Min = ow - hj
Cells(1, 10) = i
Cells(1, 11) = Min
End If
Cells(3, 10) = i
Cells(3, 11) = ow - hj
Next
End Sub
Sub zy()
この部分は同じ
End Sub
Sub f(g As Byte)
ow = Timer
If (ow - hj) > Min Then Exit Sub
If n = 4 And cn = 100 Then Exit Sub
If n = 5 And cn = 50 Then Exit Sub
Dim i As Byte, j As Byte, w As Byte, ii As Byte, iii As Byte, k As Byte
ii = Int(n * n * Rnd)
For iii = 1 To n * n
i = ((iii + ii) Mod n * n) + 1
以下同じ
参考ダウンロード添付ファイル
乱数は、シード値を指定しないと、いつも同じ順番で発生します。
乱数系列を変更するには、
シード値を指定します。
Randomize (シード値)
ただし、この前に
Rnd (-1)
によって、乱数を初期化しておく必要があります。
次のような簡単なマクロを組んで確かめて下さい。
Private Sub CommandButton1_Click()
Dim i As Byte
For i = 0 To 9
Cells(5, 2 + i) = Int(10 * Rnd)
Next
End Sub
Private Sub CommandButton2_Click()
Rows("5:20000").Select
Selection.ClearContents
Range("H4:U4").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル

確かに、実行ボタンを押す度に違う結果が出てきますが、
エクセルファイルを開いた後の1回目の結果は毎回上の画像のようになります。
実際に、エクセルを一端終了してもう一度開き実行ボタンを押して下さい。
同じ結果になっていること確認されましたか。
この乱数の出る順番=乱数系列を変更すにシード値を使います。
コードを次のように変更して下さい。
Private Sub CommandButton1_Click()
Dim i As Byte
Randomize (1)
For i = 0 To 9
Cells(5, 2 + i) = Int(10 * Rnd)
Next
End Sub
Private Sub CommandButton2_Click()
Rows("5:20000").Select
Selection.ClearContents
Range("H4:U4").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル
前回

第1回目の結果が異なっています。
さらに、コードを次のように変更した下さい。
Private Sub CommandButton1_Click()
Dim i As Byte, j As Byte
Randomize (1)
For i = 0 To 9
Randomize (1)
For j = 0 To 9
Cells(5 + i, 2 + j) = Int(10 * Rnd)
Next
Next
End Sub
Private Sub CommandButton2_Click()
Rows("5:20000").Select
Selection.ClearContents
Range("H4:U4").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル
同じシード値1を毎回指定してるので、
毎回同じ結果になるかというと、
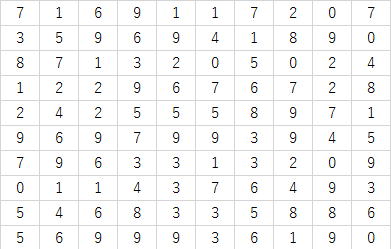
10回とも異なる結果になってしまいました。
Rnd (-1)
によって、乱数を初期化しないと乱数系列を同じにしてもダメなのです。
ですから、コードをさらに次のように変更して下さい。
Private Sub CommandButton1_Click()
Dim i As Byte, j As Byte
Randomize (1)
For i = 0 To 9
Rnd (-1)
Randomize (1)
For j = 0 To 9
Cells(5 + i, 2 + j) = Int(10 * Rnd)
Next
Next
End Sub
Private Sub CommandButton2_Click()
Rows("5:20000").Select
Selection.ClearContents
Range("H4:U4").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル
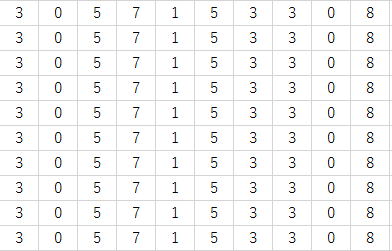
今回は10回とも同じ結果になりました。
毎回同じ系列です。
毎回系列を変更するには、
Private Sub CommandButton1_Click()
Dim i As Byte, j As Byte
Randomize (1)
For i = 0 To 9
Rnd (-1)
Randomize (i)
For j = 0 To 9
Cells(5 + i, 2 + j) = Int(10 * Rnd)
Next
Next
End Sub
Private Sub CommandButton2_Click()
Rows("5:20000").Select
Selection.ClearContents
Range("H4:U4").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
参考ダウンロード添付ファイル
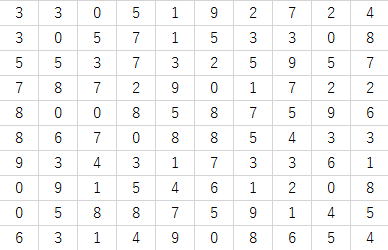
10回とも異なる結果になりました。
さらに、しかも今回は何回実行ボタンを押しても実行結果は同じになります。
Rnd (-1)でリセットするという意味お分かりになりましたか。
さて、
最適コード値探索プログラム添付ファイル
に戻りましょう。
5次魔方陣の場合、実験に時間がかかりすぎますので、
途中で中止してしまいましたが、
粘り強く実験すれば、
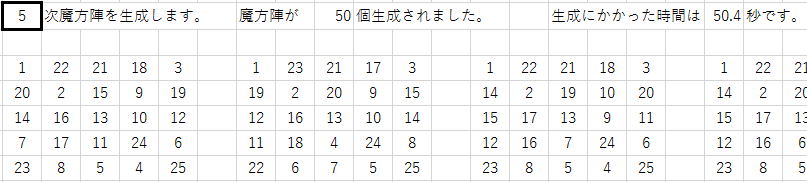
を遙かに凌駕する結果が得られるはずです。
多くのシード値で乱数を組み込んだ方が、成績が悪い理由は
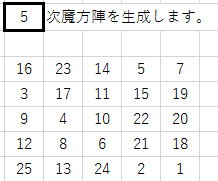
順番に入れていく方が、たまたま真ん中の数字が13になるからです。
真ん中に入れる数字で5次魔方陣を分類すると、
13のときが、一番多いのです。
理由は、各行・各列・各対角線の平均値は13なのです。
65÷5=13
ですよね。
奇数魔方陣は、真ん中のセルの数字が真ん中の数字であるとき、
数が一番多いのです。
といっても証明されてはいませんから、
予想ですが。
5次魔方陣については、
真ん中のセルの数字で分類したときに、
真ん中の数字の魔方陣数が一番多いことは、
前に実験して証明してあります。
また、3次魔方陣は真ん中のセルが真ん中の数字である5の場合しか存在していませんね。
ですから、仮説(予想)は3次と5次では証明されています。
7次以降では、仮説を証明した人は世界中を探しても誰もいません。
スパコンを使って研究しても、
6次魔方陣の総数でさえ分かっていないのです。
人類が知っている総数は5次魔方陣までなのです。
とにかく、真ん中のセルに13が入る場合が一番有利ですから、
シード値の実験では、
たまたま真ん中のセルに13になるものを探し出さなければなりませんから、
For i = 0 To 99
たった100回の試行では、見つからないかも知れません。
尚、今回は実験していませんが、
粘り強く実験を続けると、
第19講の対角線法でも10個程度であれば、
10分以内で10次魔方陣までは生成できるということは、
分かっています。
分かっているというのは、実験で確かめたことがあるということです。
皆さん、
最適コード値探索プログラム添付ファイル
を使って粘り強く実験してみて下さい。
では、対角線法による魔方陣自動生成ソフトは終わりにします。
魔方陣は、前に予告した通り、
何度も題材にして最終的には50次魔方陣であっても、
1秒に数百という単位で生成できるようにします。
第20講ではn進数演算に戻り、
減法=引き算に挑戦します。
