自然数nに対して、
 を
を で表す。たとえば
で表す。たとえば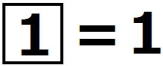 ,
,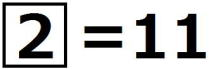 ,
,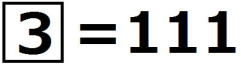 である。
である。(1) mを0以上の整数とする。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。(1)の答案その2超解説その1
第2問 2008年度 東大数学 理系 第5問
自然数nに対して、 を
を で表す。たとえば
で表す。たとえば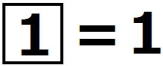 ,
,
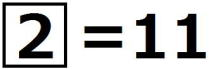 ,
,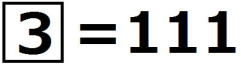 である。
である。
(1) mを0以上の整数とする。![]() は
は![]() で割り切れるが、
で割り切れるが、
![]() では割り切れないことを示せ。
では割り切れないことを示せ。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。
(1)の答案その2超解説その1
| 証明すべき命題を(*)とする。 ⅰ m=0のとき、  =1 =1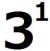 =3 =3したがって、 (*)は成り立つ。 ⅱ m=k(≧0)とき(*)が成り立つと仮定すると、  は は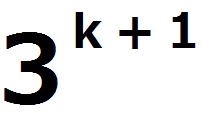 では割り切れない。 では割り切れない。 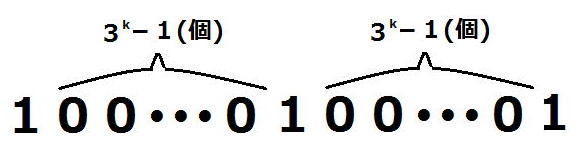 =( 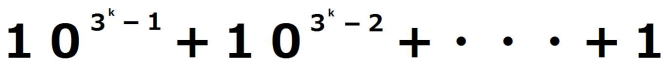 )( )(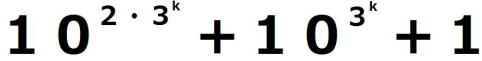 ) )= 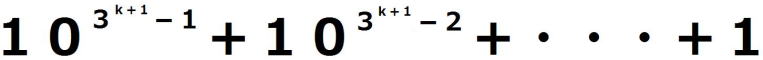 = 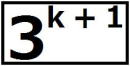 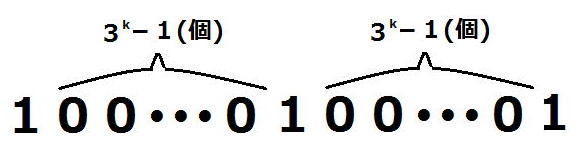 は各位の数字の和が3で3の倍数であり、 は各位の数字の和が3で3の倍数であり、9の倍数ではない。 したがって、 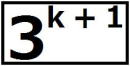 は は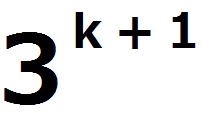 で割り切れるが、 で割り切れるが、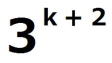 では割り切れないから、 では割り切れないから、(*)はm=k+1の場合も成り立つ。 以上ⅰⅱより、0以上のすべての整数について(*)が成り立つことが証明された。 |
(1)(2)の解答超解説を読んできた皆さんには、

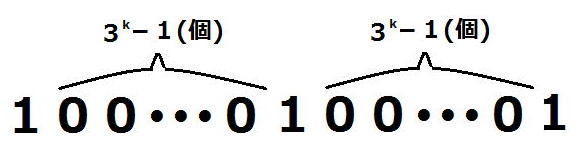
=(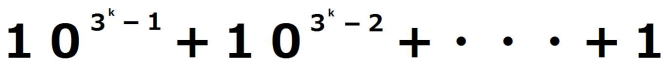 )(
)(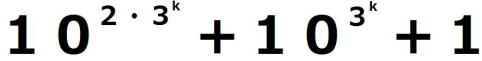 )
)
=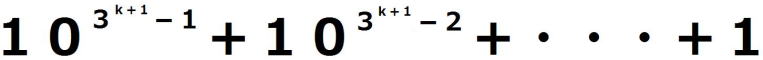
=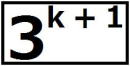
の部分のみを解説すれば十分ですよね。
もし、(1)(2)の解答超解説をお読みになっていない場合は是非お読み下さい。
例えば、111 111 111÷111を計算してみて下さい。
111 111 111÷111=1001001
です。
すなわち、
111 111 111=111×1001001です。
簡単な計算ですから、是非とも電卓を使わないで確認してみて下さい。
これは、
![]() は
は![]() で割り切れるが、
で割り切れるが、
![]() では割り切れない
では割り切れない
であるとすれば、m>0なら![]() は
は![]() で割り切れ、その商は3の倍数だろうという予測から考えています。
で割り切れ、その商は3の倍数だろうという予測から考えています。
というとかっこよすぎて、
実際には、
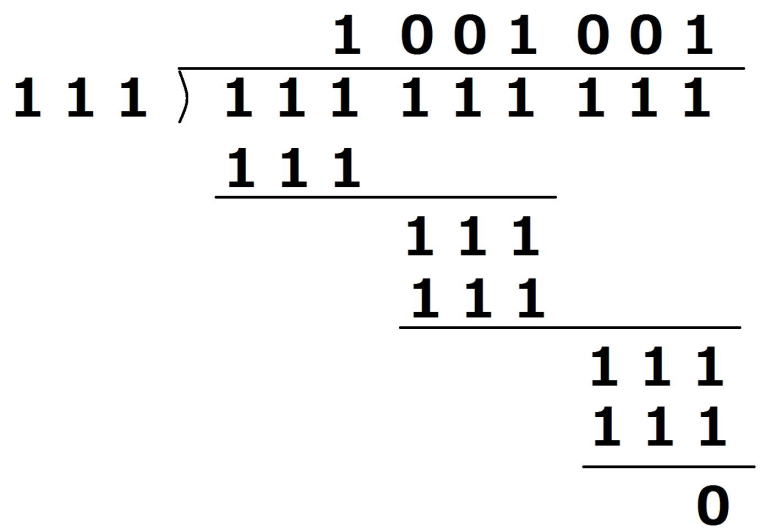
の計算をしてみて、
![]() は
は![]() で割り切れるが、
で割り切れるが、
![]() では割り切れない
では割り切れない
であるとすれば、m>0なら![]() は
は![]() で割り切れ、その商は3の倍数だろうという予測が
で割り切れ、その商は3の倍数だろうという予測が
生まれたが正しい言い方です。
『m>0なら![]() は
は![]() で割り切れ、その商は3の倍数だろう』
で割り切れ、その商は3の倍数だろう』
は当然の予測ですが、試験の現場で思いつくかといったら、
結構難しいと思いますよ。
これが思う浮かべば、(1)はあっさり落城し、
そうしたら東大の入試問題が簡単に解けることになってしまうからです。

という試行錯誤をやって着想を得た、ヒントを得たが本当のところです。
 =
=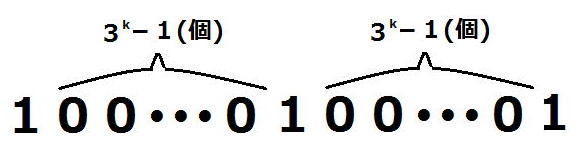 という記号を導入すれば、
という記号を導入すれば、
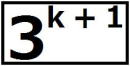 =
=
 が成立することを証明すれば、この証明は終わります。
が成立することを証明すれば、この証明は終わります。
なぜなら、 =
=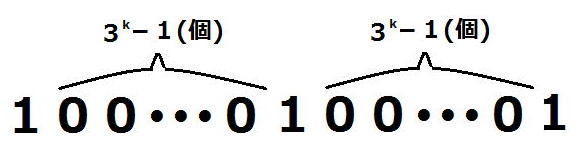 は明らかに、
は明らかに、
各位の数字の和は3で は3の倍数で9の倍数でないからです。
は3の倍数で9の倍数でないからです。
 は
は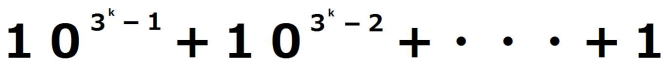 です。
です。
そもそも

がどうして成立するか分かりますか。
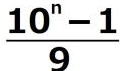 =
=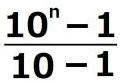 =
=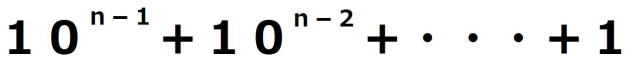
ここでは
![]() =
=
という因数分解の公式が利用されています。
aをrの置き換えれば、
![]() =
=![]()
初項が1のときの等比数列の和の公式であると考えてもいいですね。
佐藤流の受験勉強の極意をいえば、
数学はいろいろな単元と関連づけて学べです。
だからこそ、東大の入試問題は受験勉強に最適なのです。
いろいろな解法があり、それが数ⅠAⅡBⅢCの各単元と関連があり、
東大の入試問題を解いているうちに各単元の基礎が確認できるからです。
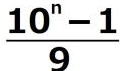 =
=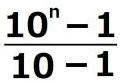 =
=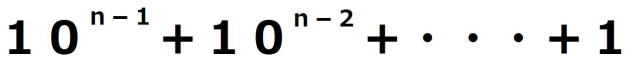 から
から
 =
=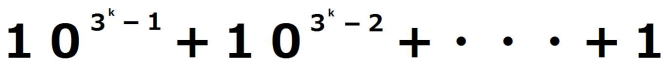
は当然ですね。
nのところに![]() を代入しただけです。
を代入しただけです。
さて、
(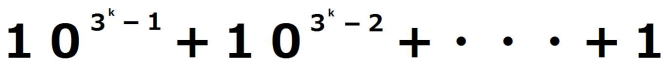 )(
)(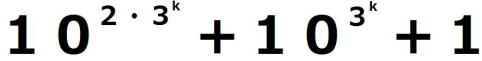 )
)
=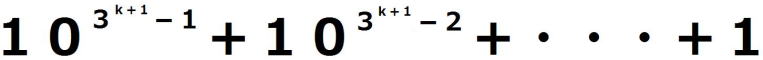
の計算ですが、
まず、 (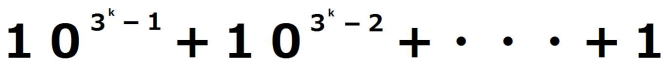 )
)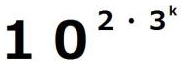
を計算してましょう。
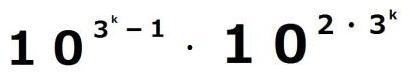 =
=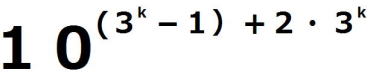
=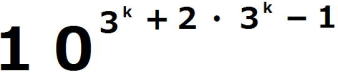
=
=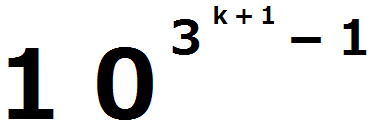
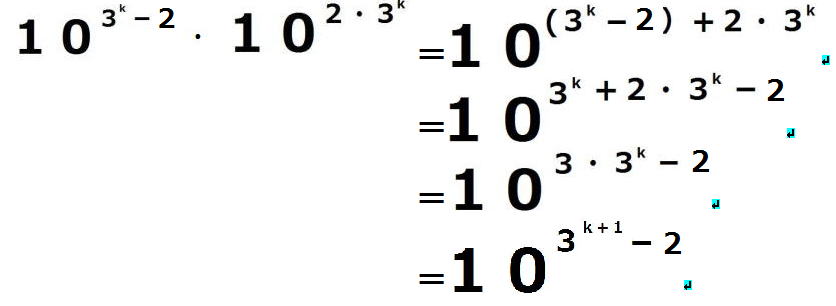
・ ・ ・
・ ・ ・
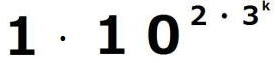 =
=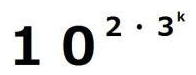
ですから、(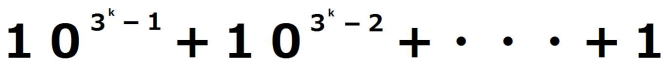 )
)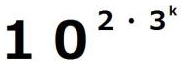 の計算結果は
の計算結果は
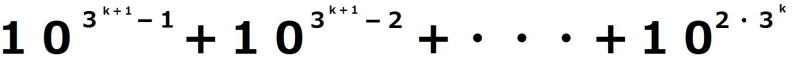
となります。次に、 (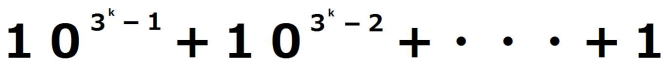 )
)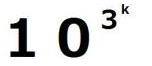 を計算してみると
を計算してみると
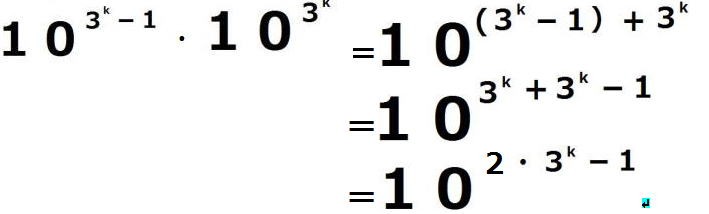
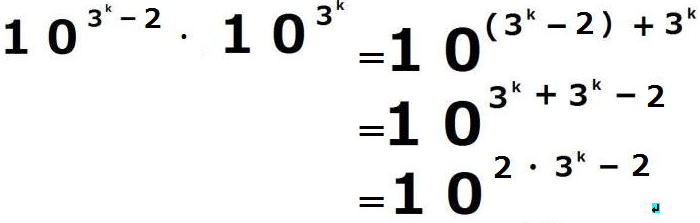
・ ・ ・
・ ・ ・
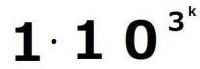 =
=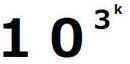
ですから、(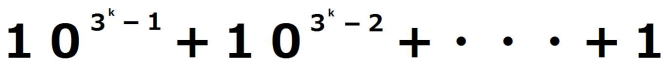 )
)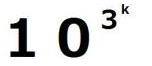 の計算結果は
の計算結果は
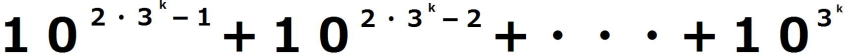
最後に(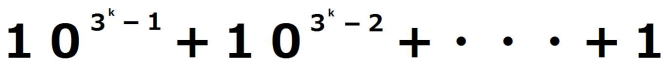 )・1の計算結果は
)・1の計算結果は
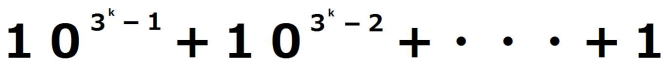 です。
です。
3つを並べてみると
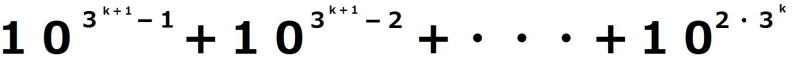
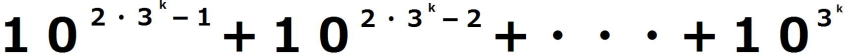
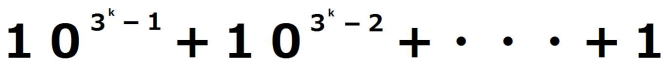
見事に連続しています。
以上から、

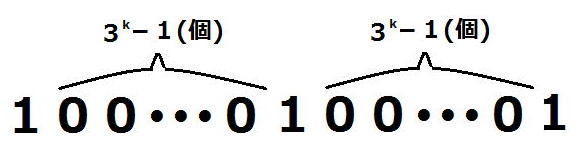
=(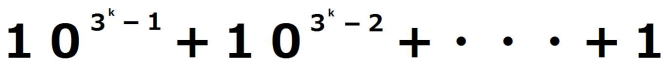 )(
)(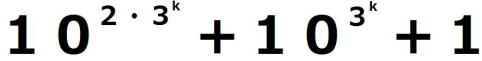 )
)
=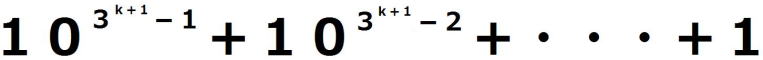
=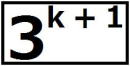
が成立するわけです。
(1)の解法その2 第3問問題へ

数独 ナンプレ 解き方 コツ 解法 難問 テクニック 研究
数独 フリーソフト 数独自動生成無料アプリ 難問 作成 プログラム
魔方陣 数独で学ぶ 初心者のための VBA 入門 基礎から応用まで
数独 ナンプレ 難問 シンプルな解き方・簡単な解法・わかりやすい攻略法の研究
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第2部
初心者のための
VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のためのEclipseによるJava入門 基礎から応用まで
初心者のためのJava入門サイト 基礎から応用まで
本サイトトップへ