自然数nに対して、
 を
を で表す。たとえば
で表す。たとえば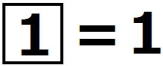 ,
,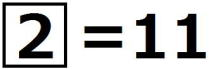 ,
,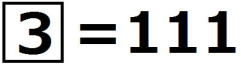 である。
である。(1) mを0以上の整数とする。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。(2)の解答その1 超解説その5(必要条件側の有力手その1)
第2問 2008年度 東大数学 理系 第5問
自然数nに対して、 を
を で表す。たとえば
で表す。たとえば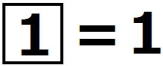 ,
,
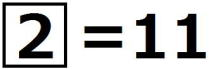 ,
,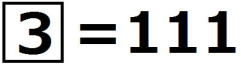 である。
である。
(1) mを0以上の整数とする。![]() は
は![]() で割り切れるが、
で割り切れるが、
![]() では割り切れないことを示せ。
では割り切れないことを示せ。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。
(2)の解答その1 超解説その5(必要条件側の有力手その1)
逆に、 が27で割り切れると仮定すると、 が27で割り切れると仮定すると、適当な自然数pによって、  =27p・・・・② =27p・・・・②と表すことができる。 しがたって、  の各位の数字の和nは9の倍数であるから、 の各位の数字の和nは9の倍数であるから、適当な自然数qによって、 n=9q・・・・③ とおくことができる。 よって、  = =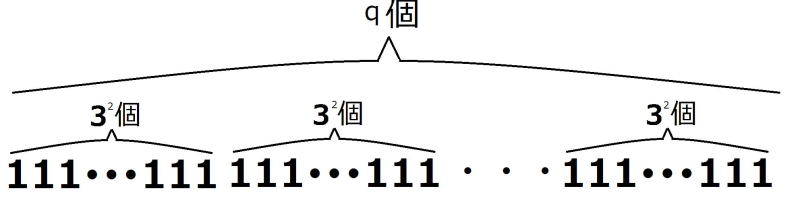 = 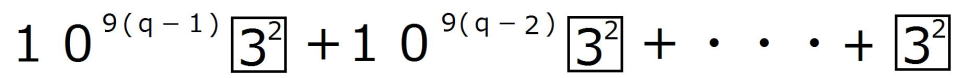 = 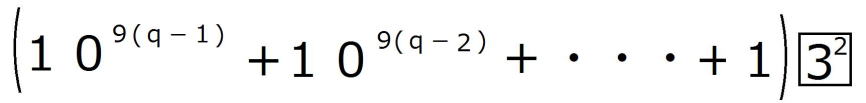 ②より 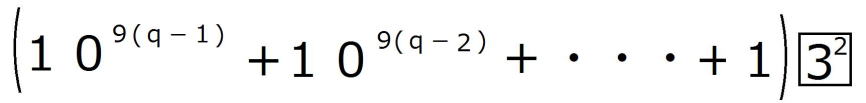 =27p =27p(1)より  は9の倍数であるが、27の倍数でないから、 は9の倍数であるが、27の倍数でないから、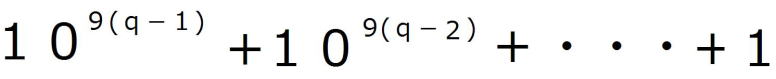 は3の倍数である。 は3の倍数である。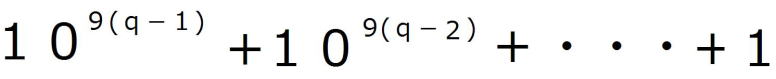 の各位の数字の和はqであるから、 の各位の数字の和はqであるから、qも3の倍数である。 よって、③からnは27の倍数である。 |
の部分の超解説その2!
グループ分け
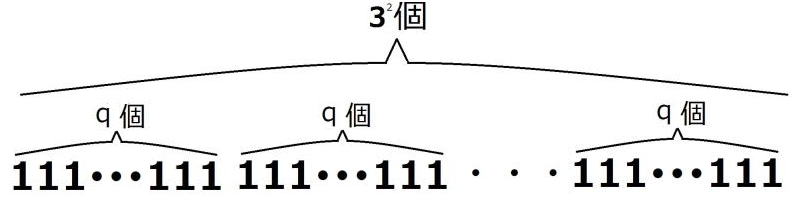
をまず、次のように分解します。
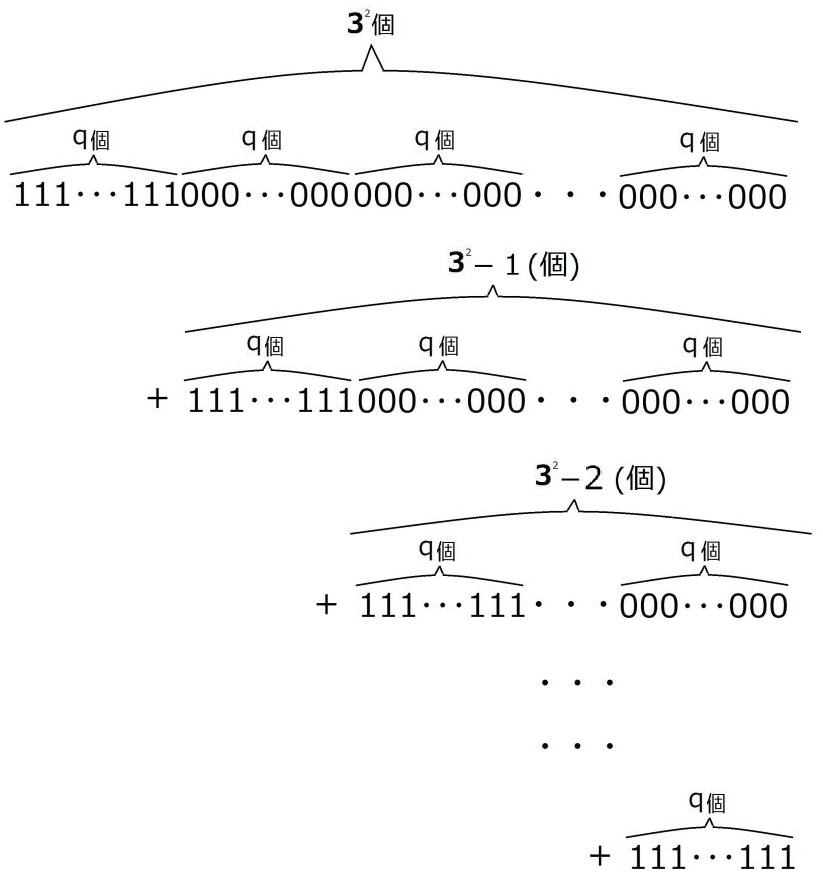
すると、
 =
=
=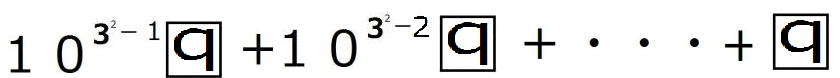
=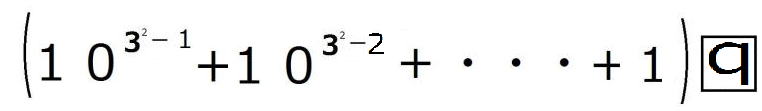
となります。
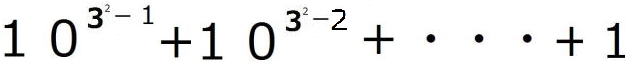
は1が![]() 個ありますから、各位の数字の和は
個ありますから、各位の数字の和は![]() で9です。
で9です。
ということは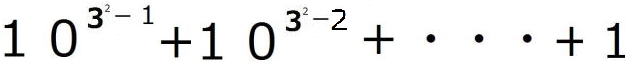 は9の倍数です。
は9の倍数です。
 は整数ですから
は整数ですから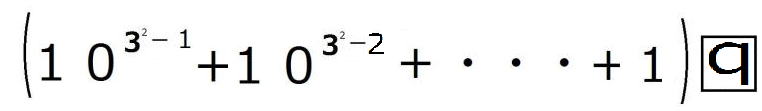 も9の倍数になり、
も9の倍数になり、
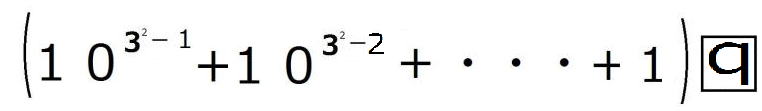 の各位の数字の和も9の倍数です。
の各位の数字の和も9の倍数です。
 の各位の数字の和
の各位の数字の和
n=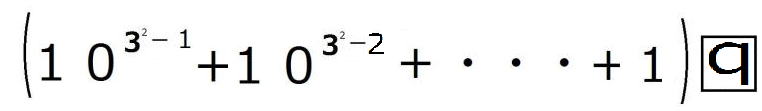 の各位の数字の和
の各位の数字の和
からnが9の倍数まではいえます。
ですが、nが27の倍数とはいえません。
後一歩ですが、踏破できませんでした。
悔しいですね。
ここでも『各位の数字の和が27の倍数であればその整数は27の倍数である』
とはいえないことが災いしています。
もし、『各位の数字の和が27の倍数であればその整数は27の倍数である』が成り立てば、
 が27の倍数で、
が27の倍数で、 の各位の数字の和nも27の倍数であると簡単にいえたわけですが、
の各位の数字の和nも27の倍数であると簡単にいえたわけですが、
『各位の数字の和が27の倍数であればその整数は27の倍数である』が成り立たないことに、
東大の先生方は注目してこの問題を作ったのでしょう。
ですから、『各位の数字の和が27の倍数であればその整数は27の倍数であるとはいえない』
ことが2008年度 東大数学 理系 第5問の最大のキモといえるでしょう。
(2)の解答その1 超解説その4へ (2)の解答その1 超解説その6へ

数独 ナンプレ 解き方 コツ 解法 難問 テクニック 研究
数独 フリーソフト 数独自動生成無料アプリ 難問 作成 プログラム
魔方陣 数独で学ぶ 初心者のための VBA 入門 基礎から応用まで
数独 ナンプレ 難問 シンプルな解き方・簡単な解法・わかりやすい攻略法の研究
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第2部
初心者のための
VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のためのEclipseによるJava入門 基礎から応用まで
初心者のためのJava入門サイト 基礎から応用まで
本サイトトップへ