自然数nに対して、
 を
を で表す。たとえば
で表す。たとえば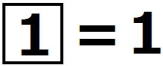 ,
,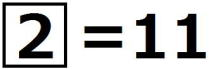 ,
,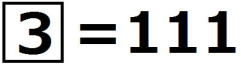 である。
である。(1) mを0以上の整数とする。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。(2)の解答その1 超解説その2(十分条件側の有力手その1)
今回はnが27で割り切れることが
 が27で割り切れることの十分条件であること
が27で割り切れることの十分条件であることの証明の超解説です。ですから、
第2問 2008年度 東大数学 理系 第5問
自然数nに対して、 を
を で表す。たとえば
で表す。たとえば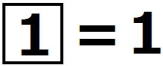 ,
,
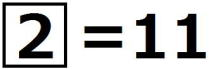 ,
,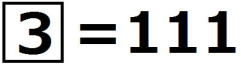 である。
である。
(1) mを0以上の整数とする。![]() は
は![]() で割り切れるが、
で割り切れるが、
![]() では割り切れないことを示せ。
では割り切れないことを示せ。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。
(2)の解答その1 超解説その2(十分条件側の有力手その1)
今回はnが27で割り切れることが が27で割り切れることの十分条件であること
が27で割り切れることの十分条件であること
の証明の超解説です。ですから、
| (2)の解答 nが27で割り切れると仮定すると、 適当な3の倍数でない整数pが存在して、 n=27p= 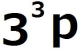 ・・・・① ・・・・①が成り立つ。 このとき、  = =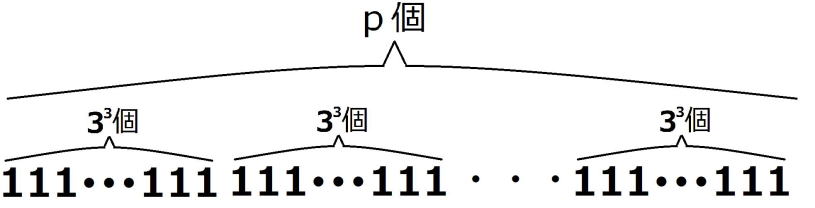 = 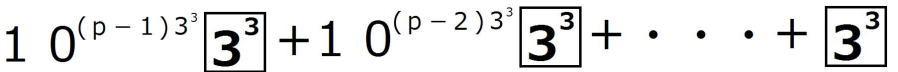 = 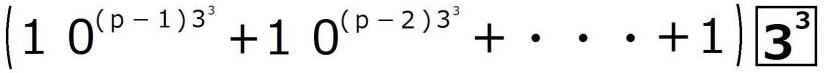 (1)より  は27で割り切れる。 は27で割り切れる。 |
の部分の超解説です。
27は![]() であることに気がつくことが肝要です。
であることに気がつくことが肝要です。
そうです。
これに気がつけば、(1)の結果を使える可能性が
あるのではないかという考えが浮かびます。
(1)は(2)のヒント---セオリーです。
では実際にはどのようにして(1)を応用するのでしょうか。
展望が見えなくても、とりあえずはセオリーにしがたい
適当な自然数によって
n=27p=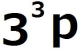 ・・・・①
・・・・①
とおいてみます。すると、 は1が
は1が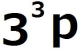 個並ぶことが分かります。
個並ぶことが分かります。
問題は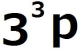 個の1をどういうグループに分けるかです。
個の1をどういうグループに分けるかです。
これは逆論証の必要条件の証明においても同じです。
グループの分け方としては、答案で採用した

と
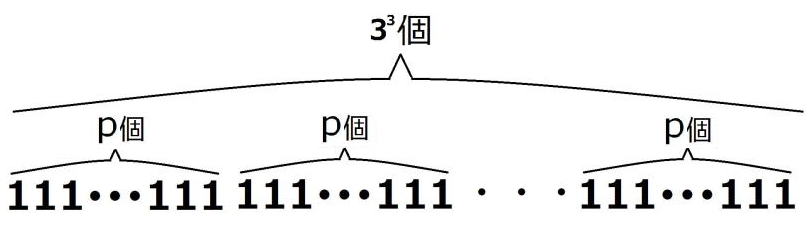
の2つが考えられます。
どちらが正しいのかは、試行錯誤でしか確認できません。
もちろん、両方ともダメである場合もあります。
でも、有力な手は試してみるしかありません。
将棋のプロの棋士は、直観で3つぐらいの有望な手を考え、
後は読み(頭の中で駒を動かす)によって、最善手を選ぶそうです。
3つとも読みによって、いい手ではないと判断すれば、
また直観を使い有力手を探すしかないわけです。
数学も全く同じです。
直観で有力手を選び、論証する---ダメであれば有力手を選び直す---
これの繰り返しです。
さて、

というグループ分けの場合どうなるでしょうか。
 を単位と考えたわけです。
を単位と考えたわけです。
 は
は![]() ですね。
ですね。

を次のように分解してみましょう。
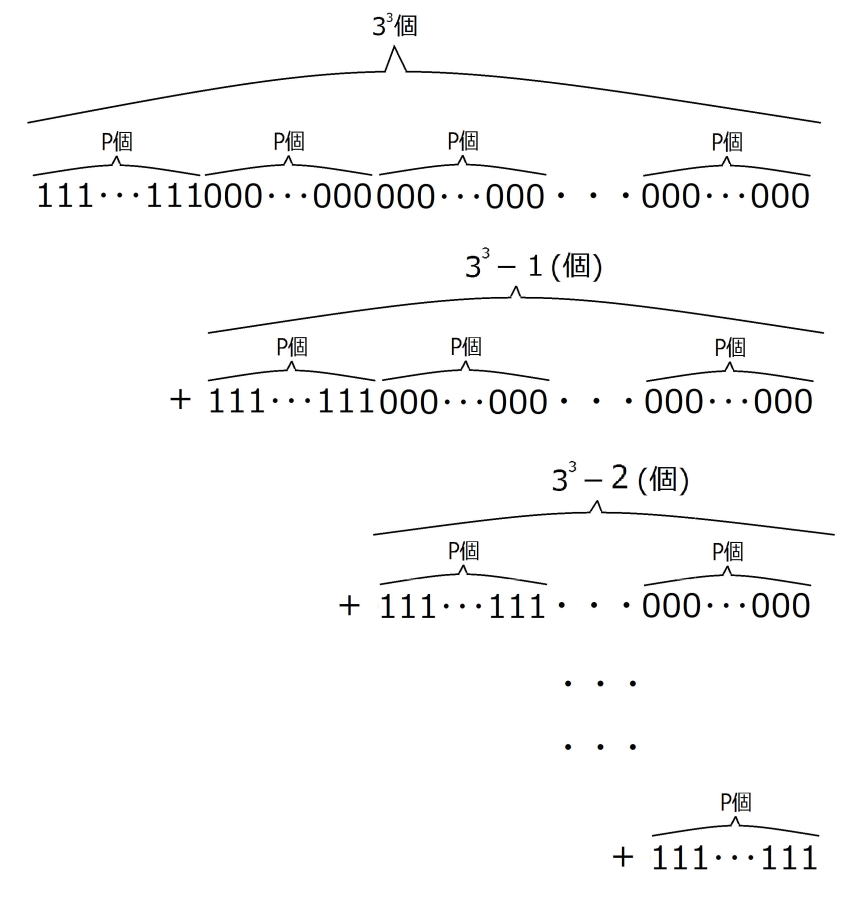
すると すなわち
すなわち は
は
 =
=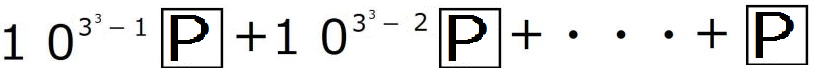
=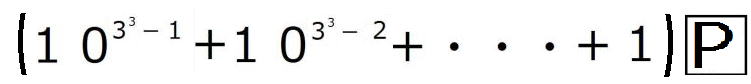
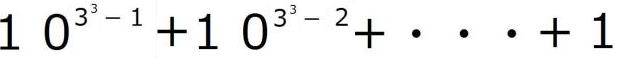 は1が
は1が![]() 個並びますから、
個並びますから、
各位の数字の和が27で9の倍数であることはいえます。
各位の数字の和が27の倍数であってもそのもとの整数が27の倍数であるはいえませんでした。
![]() の各位の数字の和はpですが、
の各位の数字の和はpですが、
| (2)の解答 nが27で割り切れると仮定すると、 適当な3の倍数でない整数pが存在して、 n=27p= 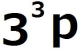 ・・・・① ・・・・① |
で断ってあった通り、pは3の倍数ではありませんから、
![]() は3の倍数ではありません。
は3の倍数ではありません。
すると、

というグループ分けだと、9の倍数までしかいえません。
27の倍数であることをいわなければなりませんので、失敗です。
(2)の解答その1 超解説その1へ (2)の解答その1 超解説その3へ

数独 ナンプレ 解き方 コツ 解法 難問 テクニック 研究
数独 フリーソフト 数独自動生成無料アプリ 難問 作成 プログラム
魔方陣 数独で学ぶ 初心者のための VBA 入門 基礎から応用まで
数独 ナンプレ 難問 シンプルな解き方・簡単な解法・わかりやすい攻略法の研究
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第2部
初心者のための
VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のためのEclipseによるJava入門 基礎から応用まで
初心者のためのJava入門サイト 基礎から応用まで
本サイトトップへ