自然数nに対して、
 を
を で表す。たとえば
で表す。たとえば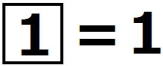 ,
,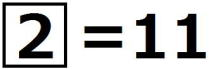 ,
,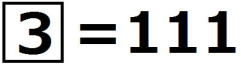 である。
である。(1) mを0以上の整数とする。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。(2)の解答その1 超解説その1(必要条件・十分条件・必要十分条件とは?)
さて、
第2問 2008年度 東大数学 理系 第5問
自然数nに対して、 を
を で表す。たとえば
で表す。たとえば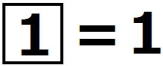 ,
,
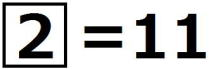 ,
,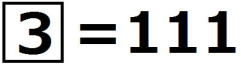 である。
である。
(1) mを0以上の整数とする。![]() は
は![]() で割り切れるが、
で割り切れるが、
![]() では割り切れないことを示せ。
では割り切れないことを示せ。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。
(2)の解答その1 超解説その1(必要条件・十分条件・必要十分条件とは?)
さて、
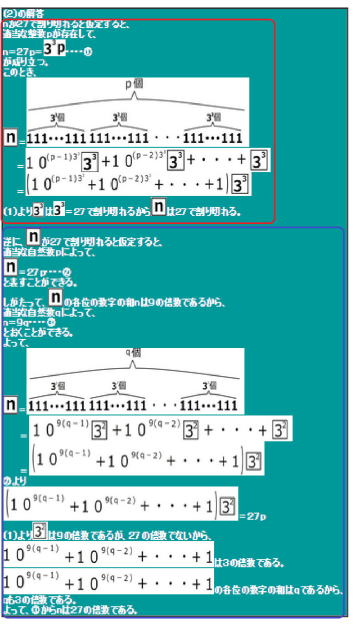
| (2)の解答 nが27で割り切れると仮定すると、 適当な3の倍数でない整数pが存在して、 n=27p= 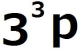 ・・・・① ・・・・①が成り立つ。 このとき、  = =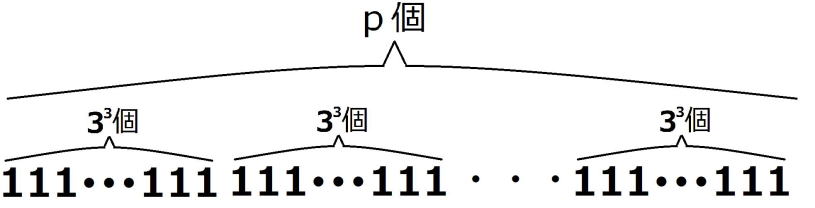 = 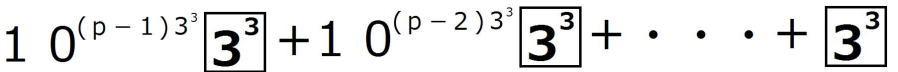 = 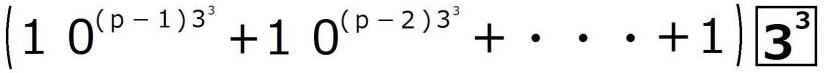 (1)より  は27で割り切れる。 は27で割り切れる。逆に、  が27で割り切れると仮定すると、 が27で割り切れると仮定すると、適当な自然数pによって、  =27p・・・・② =27p・・・・②と表すことができる。 しがたって、  の各位の数字の和nは9の倍数であるから、 の各位の数字の和nは9の倍数であるから、適当な自然数qによって、 n=9q・・・・③ とおくことができる。 よって、  = =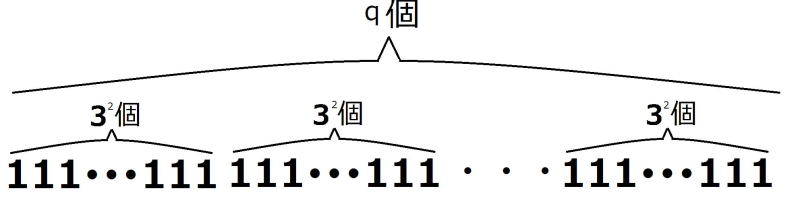 = 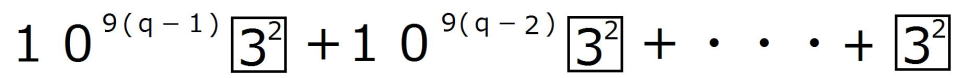 = 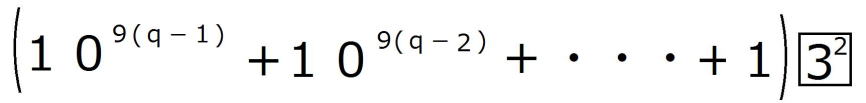 ②より 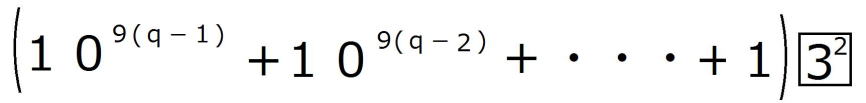 =27p =27p(1)より  は9の倍数であるが、27の倍数でないから、 は9の倍数であるが、27の倍数でないから、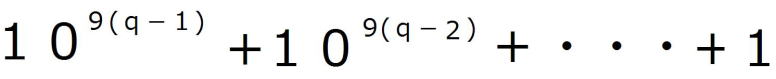 は3の倍数である。 は3の倍数である。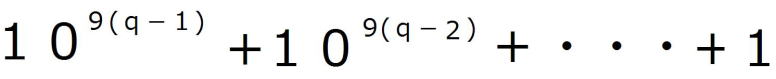 の各位の数字の和はqであるから、 の各位の数字の和はqであるから、qも3の倍数である。 よって、③からnは27の倍数である。 |
を超解説しましょう。
この意味不明に思える答案も超解説を読めばすっきり分かるはずです。
ここでも細部の解説に入る前に、基礎事項を確認しましょう。
皆さん、必要十分条件って何ですか。
皆さんは、この言葉の意味を2重に理解できていますか。
2重とは論理的・形式的に理解すると同時に、
直観(直感)的に理解し内容をイメージするということです。
直観的に理解し内容をイメージするとは、
言葉を聞いた瞬間に、語感から分かるということです。
おそらく形式的には理解していても意味は十全には理解していない方が圧倒的ではないでしょうか。
形式は分かるが内容はイメージできない!
論理的には理解できるが直感的には分からない!
これでは数学を理解しているとはいえません。
真の理解とは、論理的理解・形式的理解・抽象的理解+直観的理解・内容的理解・具体的理解でなければなりません。
ですが、残念ながら日本の高校生は数学が得意であったとしても、
その理解は抽象や形式の領域にとどまっていて、
直観のレベルに達していません。
物理学科の学生がイメージの伴わない数学操作をしているなら、
物理学科の教授からしかられます。
微分方程式を操作しているとき、
物理学者の頭脳には自然のイメージがありありと浮かびます。
経済学者が微分方程式を操作しているときにも、
経済的対象がありありと浮かびます。
本来は、数学も同じです。
数式をいじっているときありありと内容がイメージできなければならないのです。
ところがどうですか。
ほとんどの生徒は、数式を操作しているときイメージが全く働いていないのではないですか。
あなたが論理のレベルにとどまり、直観の領域に達していないなら、
それは真の理解ではありません。
さて、前置きはそれぐらいにして、
必要条件・十分条件の定義を確認しましょう。
pならqであるが真であるとき、
pをqであるための十分条件
qをpであるための必要条件
といいます。
pと満たす集合をP、qを満たす集合をQとしてペン図に表すと、
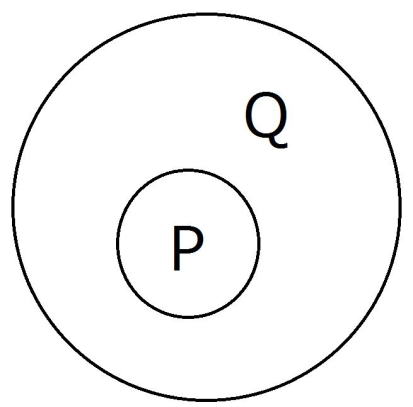
すなわち、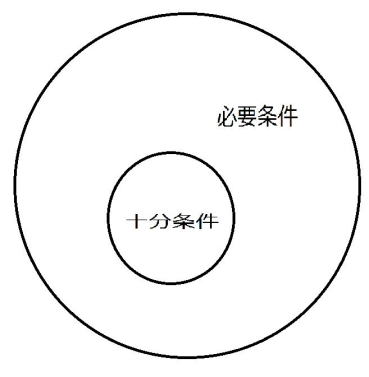 ということになります。
ということになります。

なぜこの状態のときpを十分条件、qを必要条件というのでしょうか。
理由は簡単です。
Qの中に入るには、Pに中に入れば十分です。
Pの中に入れば文句なしにQの中に入ります。
Pに入っていれば、他の条件は一切いりません。
だから、Pに入ることは十分な条件なのです。
Pの中に入るためには、Qの中には入っている必要があります。
Qの外に出てしまえば絶対にPの中には入れません。
ですが、Qの中に入っても十分ではありません。
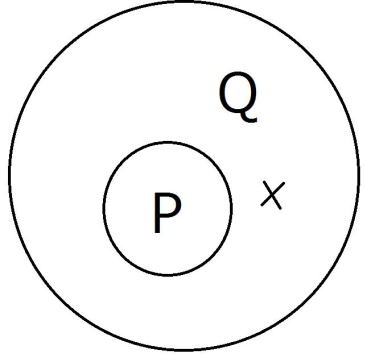
 はQの中に入っていますが、
はQの中に入っていますが、
Pの中には入りません。
ですから、qは必要な条件ですが十分な条件ではありません。
他の条件が加えられなければなりません。
必要十分条件は
pならqであるが真であると同時に、
qならpであるが真であるとき、
pをqであるための必要十分条件
qをpであるための必要十分条件
といいます。
(集合のペン図にすると、

2つの円が同じ大きさになり重なります。)
ですから、
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。
は
 が27で割り切れるならばnは27で割り切れる
が27で割り切れるならばnは27で割り切れる
nが27で割り切れるならば は27で割り切れる
は27で割り切れる
の2つを示せば良いのです。
赤い囲いが前半
nが27で割り切れるならば は27で割り切れる
は27で割り切れる
を示し、
青い囲いが後半
nが27で割り切れるならば は27で割り切れる
は27で割り切れる
を示しています。
(2)の解答その1へ (2)の解答その1 超解説その2へ

数独 ナンプレ 解き方 コツ 解法 難問 テクニック 研究
数独 フリーソフト 数独自動生成無料アプリ 難問 作成 プログラム
魔方陣 数独で学ぶ 初心者のための VBA 入門 基礎から応用まで
数独 ナンプレ 難問 シンプルな解き方・簡単な解法・わかりやすい攻略法の研究
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第2部
初心者のための
VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のためのEclipseによるJava入門 基礎から応用まで
初心者のためのJava入門サイト 基礎から応用まで
本サイトトップへ