自然数nに対して、
 を
を で表す。たとえば
で表す。たとえば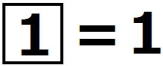 ,
,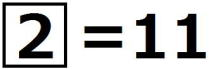 ,
,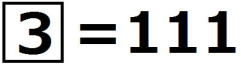 である。
である。(1) mを0以上の整数とする。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。(1)の超解説その4(数学的帰納法の簡単な例題)
第2問 2008年度 東大数学 理系 第5問
自然数nに対して、 を
を で表す。たとえば
で表す。たとえば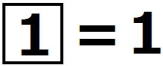 ,
,
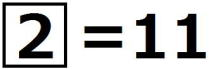 ,
,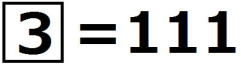 である。
である。
(1) mを0以上の整数とする。![]() は
は![]() で割り切れるが、
で割り切れるが、
![]() では割り切れないことを示せ。
では割り切れないことを示せ。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。
(1)の超解説その4(数学的帰納法の簡単な例題)
| ⅰ n=6のとき命題が成り立つことを示す。 ⅱ n=kのとき命題が成り立つと仮定すると、n=k+2でも成り立つことを示す。 |
このときの結論は
『ⅰⅱより6以上のすべての偶数について命題が成り立つ。』
となります。
例えば、
| ⅰ n=5のとき命題が成り立つことを示す。 ⅱ n=kのとき命題が成り立つと仮定すると、n=k+2でも成り立つことを示す。 |
なら、
『ⅰⅱより5以上のすべての奇数について命題が成り立つ。』
が結論ですね。
さらに、数学的帰納法には次のようなバージョンもあります。
| ⅰ n=1,2のとき命題が成り立つことを示す。 ⅱ n=kとn=k+1のそれぞれについて命題が成り立つと仮定すると、n=k+2でも成り立つことを示す。 以上ⅰⅱより、すべての自然数について命題が成り立つ。 |
では、オーソドックスな
| ⅰ n=1のとき命題が成り立つことを示す。 ⅱ n=kのとき命題が成り立つと仮定すると、n=k+1でも成り立つことを示す。 以上ⅰⅱから、すべての自然数について命題が成り立つと宣言する。 |
を応用する簡単な例題を見てみましょう。
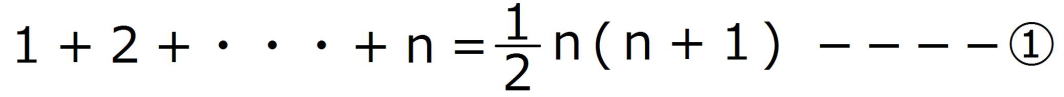
が成り立つことを数学的帰納法で証明せよ。
[証明]
ⅰ n=1のとき、
左辺=1
右辺=1/2×1×(1+1)=1
ゆえに、①は成り立つ。
ⅱ n=kのとき①が成り立つと仮定すると
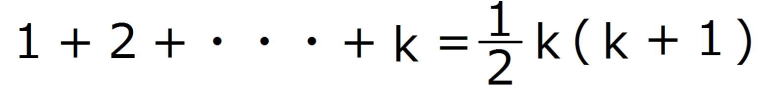
n=k+1の場合を考えると、
左辺=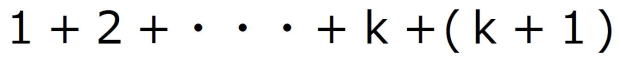
=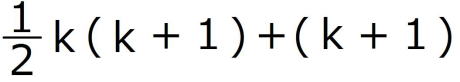
=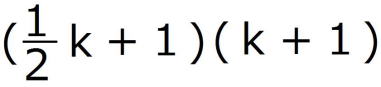
=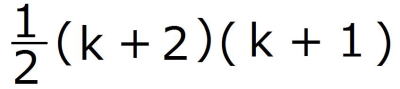
=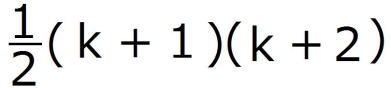
=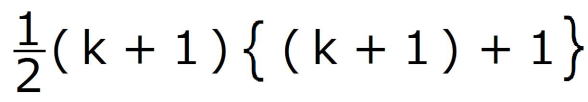
したがって、①はn=k+1の場合にも成り立つ。
以上ⅰⅱより、すべての自然数nについて①が成り立つ。
では、次の問題をやってみましょう。
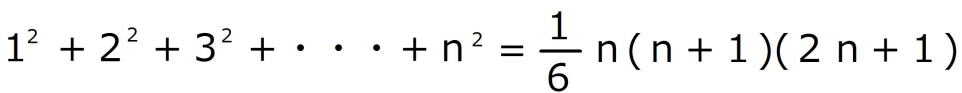
が成り立つことを数学的帰納法で証明せよ。
(1)の解答その1超解説その3へ (1)の解答その1超解説その5へ

数独 ナンプレ 解き方 コツ 解法 難問 テクニック 研究
数独 フリーソフト 数独自動生成無料アプリ 難問 作成 プログラム
魔方陣 数独で学ぶ 初心者のための VBA 入門 基礎から応用まで
数独 ナンプレ 難問 シンプルな解き方・簡単な解法・わかりやすい攻略法の研究
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第2部
初心者のための
VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のためのEclipseによるJava入門 基礎から応用まで
初心者のためのJava入門サイト 基礎から応用まで
本サイトトップへ