自然数nに対して、
 を
を で表す。たとえば
で表す。たとえば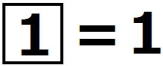 ,
,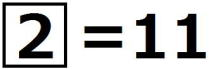 ,
,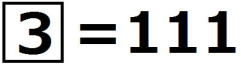 である。
である。(1) mを0以上の整数とする。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。(1)の超解説その3(数学的帰納法の説明)
第2問 2008年度 東大数学 理系 第5問
自然数nに対して、 を
を で表す。たとえば
で表す。たとえば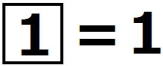 ,
,
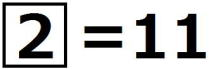 ,
,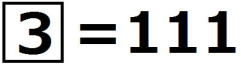 である。
である。
(1) mを0以上の整数とする。![]() は
は![]() で割り切れるが、
で割り切れるが、
![]() では割り切れないことを示せ。
では割り切れないことを示せ。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。
(1)の超解説その3(数学的帰納法の説明)
|
(1)の命題を(*)とし、(*)が成り立つことを数学的帰納法で示す。 ⅰ m=0のとき、  =1 =1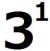 =3 =3したがって、 (*)は成り立つ。 ⅱ m=k(≧0)とき(*)が成り立つと仮定すると、  は は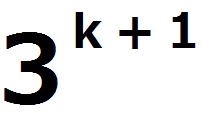 では割り切れないから、 では割り切れないから、3で割り切れない適当な整数pが存在して、  =p =pm=k+1の場合を考える。 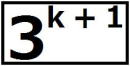 = = =  = 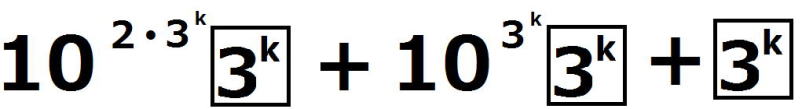 = 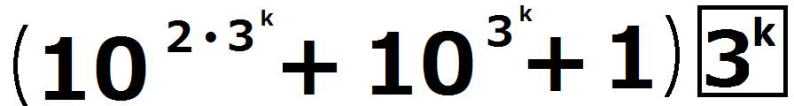 ここで、 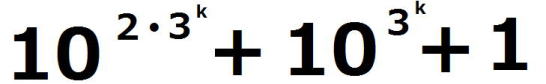 の各位の数字の和は3なので、 の各位の数字の和は3なので、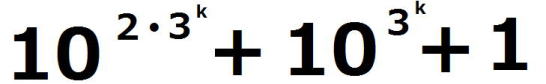 は3の倍数であるが、9の倍数ではない。 は3の倍数であるが、9の倍数ではない。よって、3で割り切れない整数qによって 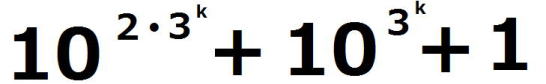 =3q =3qとおける。このとき 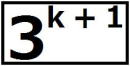 =3q・p =3q・p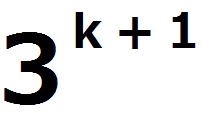 p,qは3の倍数でないので、適当な整数a,bによって、 p=3a±1,q=3b±1 と表せる。4つの組み合わせ pq=3(3ab+a+b)+1,3(3ab-a+b)-1,3(3ab+a-b)-1,3(3ab-a-b)+1 はいずれも3の倍数ではない。 したがって、 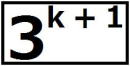 は は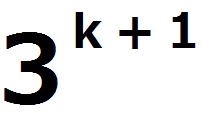 で割り切れるが、 で割り切れるが、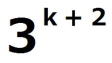 では割り切れないから、 では割り切れないから、(*)はm=k+1の場合も成り立つ。 以上ⅰⅱより、0以上のすべての整数について(*)が成り立つことが証明された。 |
を超解説する!
細部の説明に入る前に数学的帰納法の枠組みを確認しておきましょう。
数学的帰納法とは、次の3段手続きによって証明する方法です。
| ⅰ n=1のとき命題が成り立つことを示す。 ⅱ n=kのとき命題が成り立つと仮定すると、n=k+1でも成り立つことを示す。 以上ⅰⅱから、すべての自然数について命題が成り立つと宣言する。 |
なぜ、これで命題がすべての自然数ついて成り立つといえるでしょうか。
これは将棋倒し(ドミノ倒し)であると思えば良いのです。
ⅰでは、将棋の1枚目の駒(ドミノの1枚目)が倒れることを証明します。
ⅱでは、n枚目の駒が倒れると仮定すると、n+1枚目が倒れることを証明します。
この2つによって、すべての駒が倒れることが証明されます。
???どうして?
ポイントは、
ⅱでは、『n枚目の駒が倒れると仮定すると、n+1枚目が倒れることを証明します。』
の赤のところが抽象的なnとなっているところです。
このnは自然数であれば何でも変身します。
場合によってはnは1になりますし、2にも3にも4にも・・・1万にもなります。
例えば、nが1に変身するとき、
1枚目の駒が倒れると仮定すると、1+1枚目が倒れる
=1枚目の駒が倒れると仮定すると、2枚目が倒れる
nが2に変身するとき、
2枚目の駒が倒れると仮定すると、2+1枚目が倒れる
=2枚目の駒が倒れると仮定すると、3枚目が倒れる
nが3に変身するとき、
3枚目の駒が倒れると仮定すると、3+1枚目が倒れる
=3枚目の駒が倒れると仮定すると、4枚目が倒れる
nが4に変身するとき、
4枚目の駒が倒れると仮定すると、4+1枚目が倒れる
=4枚目の駒が倒れると仮定すると、5枚目が倒れる
・
・
・
と無限に続いていきます。
つまり、ⅱが言っていることは、
1枚目が倒れれば、2枚目が倒れる
2枚目が倒れれば、3枚目が倒れる
3枚目が倒れれば、4枚目が倒れる
4枚目が倒れれば、5枚目が倒れる
・
・
・
ということです。
そして、ⅰによって1枚目が倒れることが保証されているのです。
ⅰとⅱを合わせれば、すべての駒が倒れることが証明されます。
ⅰでは、将棋の1枚目の駒(ドミノの1枚目)が倒れることを証明します。
ⅱでは、n枚目の駒が倒れると仮定すると、n+1枚目が倒れることを証明します。
を
ⅰ n=1のとき命題が成り立つことを証明する。
ⅱ n=kのとき命題が成り立つと仮定すると、n=k+1でも成り立つことを証明する。
と書き換えれば、ⅱでは、
n=1のとき成り立てば、n=2でも成り立つ。
n=2のとき成り立てば、n=3でも成り立つ。
n=3のとき成り立てば、n=4でも成り立つ。
n=4のとき成り立てば、n=5でも成り立つ。
・
・
・
と無限に続きます。
そして、ⅰではn=1のとき、成り立つことが保証されています。
ⅰとⅱを合わせれば、命題はすべての自然数について成り立つことがいえるわけです。
| ⅰ n=1のとき命題が成り立つことを示す。 ⅱ n=kのとき命題が成り立つと仮定すると、n=k+1でも成り立つことを示す。 以上ⅰⅱから、すべての自然数について命題が成り立つと宣言する。 |
によって確かにすべての自然数について成り立つことが分かると思います。
尚、命題の始まりは1でなくてもよくて、n=1をn=0とすれば
| ⅰ n=0のとき命題が成り立つことを示す。 ⅱ n=kのとき命題が成り立つと仮定すると、n=k+1でも成り立つことを示す。 以上ⅰⅱから、0以上のすべての整数について命題が成り立つと宣言する。 |
0以上のすべての整数について成り立つことになります。
また、
| ⅰ n=6のとき命題が成り立つことを示す。 ⅱ n=kのとき命題が成り立つと仮定すると、n=k+2でも成り立つことを示す。 |
のようなバリエーションもあります。
このときの結論は何ですか。
(1)の解答その1超解説その2へ (1)の解答その1超解説その4へ

数独 ナンプレ 解き方 コツ 解法 難問 テクニック 研究
数独 フリーソフト 数独自動生成無料アプリ 難問 作成 プログラム
魔方陣 数独で学ぶ 初心者のための VBA 入門 基礎から応用まで
数独 ナンプレ 難問 シンプルな解き方・簡単な解法・わかりやすい攻略法の研究
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第2部
初心者のための
VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のためのEclipseによるJava入門 基礎から応用まで
初心者のためのJava入門サイト 基礎から応用まで
本サイトトップへ