第2問 2008年度 東大数学 理系 第5問
自然数nに対して、 を
を で表す。たとえば
で表す。たとえば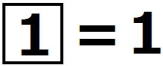 ,
,
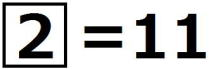 ,
,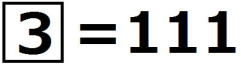 である。
である。
(1) mを0以上の整数とする。 は
は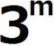 で割り切れるが、
で割り切れるが、
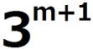 では割り切れないことを示せ。
では割り切れないことを示せ。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。
(1)の超解説その2
『各位の数字の和が27の倍数ならその整数は27の倍数である』
の反例
5877の各位の数字の和は
5+8+7+7=27で27の倍数ですが、
5877÷27=217・・・18
で5877は27の倍数ではありません。
では次に、『各位の数字の和が27の倍数でないならその整数は27の倍数でない』
の反例はどうでしょうか。
27が反例ですね。
2+7=9で27の倍数ではありませんが、
27は27の倍数です。
『各位の数字の和が27の倍数でないならその整数は27の倍数でない』は、
『各位の数字の和が27の倍数でないならその整数は27の倍数でない』の対偶ですから、
成り立たないのは当然です。
では、 =
= =111111111が27で割り切れないことを示すにはどうしたらよいでしょうか。
=111111111が27で割り切れないことを示すにはどうしたらよいでしょうか。
解答のようにやっても良いわけですが、
単純に111111111÷27を計算すると、
商が4115226で余りが9で、割り切れません。
さて、ではいよいよ解答の
(1)の命題を(*)とし、(*)が成り立つことを数学的帰納法で示す。
ⅰ m=0のとき、
 = = = = =1 =1
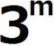 = = =1 =1
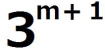 = =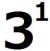 =3 =3
したがって、 は は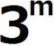 で割り切れが、 で割り切れが、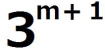 では割り切れないから では割り切れないから
(*)は成り立つ。
ⅱ m=k(≧0)とき(*)が成り立つと仮定すると、
 は は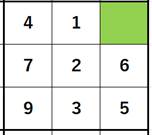 で割り切れるが、 で割り切れるが、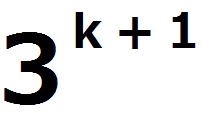 では割り切れないから、 では割り切れないから、
3で割り切れない適当な整数pが存在して、
 =p =p
m=k+1の場合を考える。
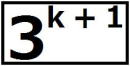 = =
=
=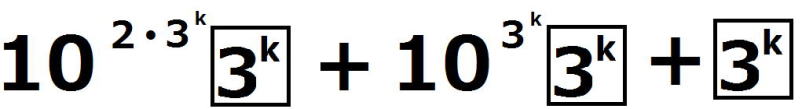
=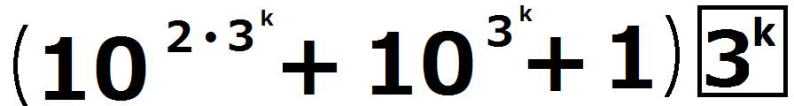
ここで、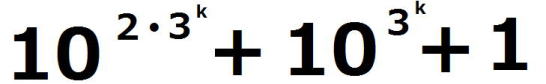 の各位の数字の和は3なので、 の各位の数字の和は3なので、
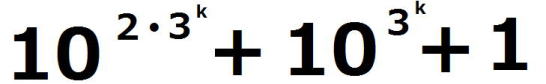 は3の倍数であるが、9の倍数ではない。 は3の倍数であるが、9の倍数ではない。
よって、3で割り切れない整数qによって
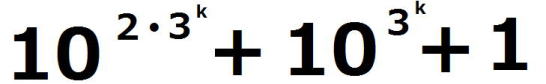 =3q =3q
とおける。このとき
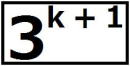 =3q・p =3q・p =pq =pq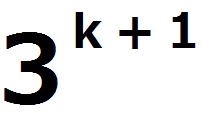
p,qは3の倍数でないので、適当な整数a,bによって、
p=3a±1,q=3b±1
と表せる。4つの組み合わせ
pq=3(3ab+a+b)+1,3(3ab-a+b)-1,3(3ab+a-b)-1,3(3ab-a-b)+1
はいずれも3の倍数ではない。
したがって、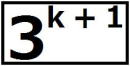 は は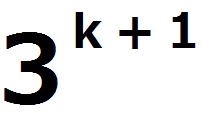 で割り切れるが、 で割り切れるが、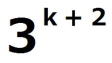 では割り切れないから、 では割り切れないから、
(*)はm=k+1の場合も成り立つ。
以上ⅰⅱより、0以上のすべての整数について(*)が成り立つことが証明された。 |
の部分の超解説に入りましょう。
(1)の解答その1超解説その1へ (1)の解答その1超解説その3へ

数独 ナンプレ 解き方 コツ 解法 難問 テクニック 研究
数独 フリーソフト 数独自動生成無料アプリ 難問 作成 プログラム
魔方陣 数独で学ぶ 初心者のための VBA 入門 基礎から応用まで
数独 ナンプレ 難問 シンプルな解き方・簡単な解法・わかりやすい攻略法の研究
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第2部
初心者のための
VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のためのEclipseによるJava入門 基礎から応用まで
初心者のためのJava入門サイト 基礎から応用まで
本サイトトップへ
 を
を で表す。たとえば
で表す。たとえば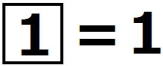 ,
,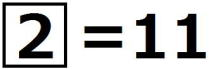 ,
,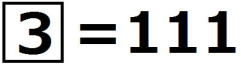 である。
である。 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。 =111111111が27で割り切れないことを示すにはどうしたらよいでしょうか。
=111111111が27で割り切れないことを示すにはどうしたらよいでしょうか。 =1
=1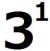 =3
=3 は
は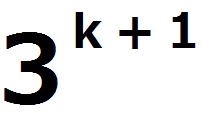 では割り切れないから、
では割り切れないから、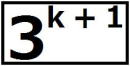 =
=

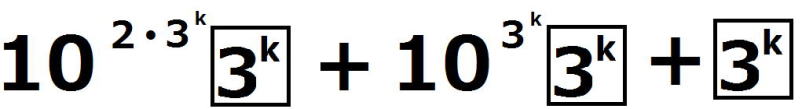
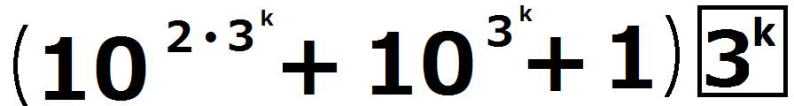
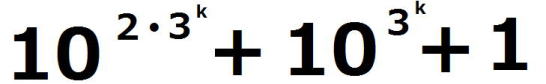 の各位の数字の和は3なので、
の各位の数字の和は3なので、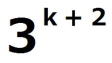 では割り切れないから、
では割り切れないから、