自然数ｎに対して、
を
で表す。たとえば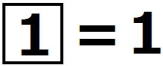
，
，
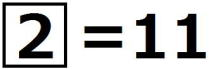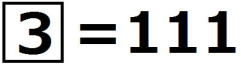である。（１） ｍを0以上の整数とする。
は
で割り切れるが、
では割り切れないことを示せ。（２） ｎが２７で割り切れることが、
が２７で割り切れるための必要十分条件であることを示せ。（１）の超解説その１
この問題の要所は、
との意味の違いを理解することです。とは何でしょうか。意味が分からないときは、必ずいったんは具体化しましょう。
ｍ＝０のとき、
＝
＝
＝１＝
＝１ｍ＝１のとき、
＝
＝
＝１１１＝
＝３ｍ＝２のとき、
＝
＝
＝１１１１１１１１１＝
＝９ｍ＝３のとき、
＝
＝
＝１１１ １１１ １１１ １１１ １１１ １１１ １１１ １１１ １１１＝
＝２７例えば、
＝１１１１１１１１１は＝９で割り切れます。理由は１１１１１１１１１の各位の数字の和は
１＋１＋１＋１＋１＋１＋１＋１＋１＝９
で９の倍数であるからです。
『各位の数字の和が９の倍数である場合、
その整数は９の倍数である』でしたね。
（裏命題
『各位の数字の和が９の倍数でない場合、
その整数は９の倍数でない』も
逆命題
『整数が９の倍数である場合、
各位の整数の和は９の倍数である』も成立します。）
肝要なことは
＝の９は１が９個並ぶということです。ということは各位の数字の和が９になるということです。
すなわち、
における各位の数字の和はｎです。＝なら各位の数字の和は２７です。さて、
＝＝＝１１１１１１１１１は
＝＝２７で割り切れないのでしょうか。３の倍数や９の倍数の判定法から、
『各位の数字の和が２７の倍数ならその整数は２７の倍数である』と
裏命題『各位の数字の和が２７の倍数でないならその整数は２７の倍数でない』
さらに、逆命題『整数が２７の倍数なら、各位の数字の和は２７の倍数である』
の成立を予想される方もいらっしゃるでしょうが、
これは正しい予想でしょうか。
これが正しければ、
＝＝＝１１１１１１１１１の各位の数字の和は９で２７の倍数でないわけですから、
は２７の倍数でないといえるわけですが、『各位の数字の和が２７の倍数ならその整数は２７の倍数である』
『各位の数字の和が２７の倍数でないならその整数は２７の倍数でない』
『整数が２７の倍数なら、各位の数字の和は２７の倍数である』
は、実はいずれも成り立ちません。
『整数が２７の倍数なら、各位の数字の和は２７の倍数である』
の反証は簡単です。
２７は２７の倍数ですが、各位の数字の和は２＋７＝９です。
反例が一つでも存在すれば命題は成立しないのでしたね。
では、『各位の数字の和が２７の倍数ならその整数は２７の倍数である』
の反例はあるでしょうか。
この問題の要所のもうひとつを付け加えておきましょう。
これも（１）と（２）に共通のキモといえます。
は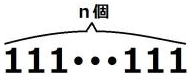
と１がｎ個並ぶ数字です。注目すべき点は、各位の数字の和１＋１＋１＋・・・＋１＝ｎという点です。
＝１１１を例に取れば、
１＋１＋１＝３
です。
はであり、の各位の数字の和はｎです。と各位の数字の和であるｎを行ったり来たりする、２つの次元を行ったり来たりすることが最大のミソです。
すなわちとｎを明確に区別することがとても肝要です。とｎは全く別のものです。を例に取れば、１１１と３です。別のものというのを強調するために『２つの次元を行ったり来たりする』の比喩を入れたわけです。
とｎを明確に区別して読まないと、解答にしても超解説にしても、頭が混乱してしまいます。
（１）の解答その１へ （１）の解答その１超解説その２へ
数独 ナンプレ 解き方 コツ 解法 難問 テクニック 研究
