第２話 ガウスの素数研究
19世紀になると、素数研究に時期を画す研究がガウスによって展開されます。
素数定理に関する予想です。
この予想は、
1896年にシャルル＝ジャン・ド・ラ・ヴァレー・プーサンとジャック・アダマールによって、
独立に証明されています。
ガウスの予想とは、π（ｘ）〜ｘ／ｌｏｇ ｘです。
π（ｘ）は整数ｘまでにある素数の個数を表す関数ですし、
〜はおよそ等しいという意味です。
π（ｘ）をイメージするためにいくかの値を示してみましょう。
π（０）＝０，π（１）＝０，π（２）＝１，π（３）＝２，π（４）＝２，
π（５）＝３，π（６）＝３，π（７）＝４，π（８）＝４，・・・
素数のときに、段が１段上がりますので素数階段といいます。
π（８）＝４は整数１から８までに素数が４つあることを示しています。
実際に、１，２，３，４，５，６，７，８ 素数の数を数えると４個ですね。
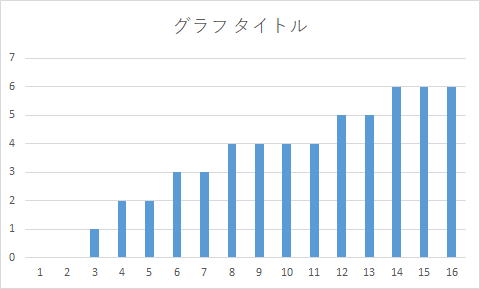
素数階段（横軸がｘ、縦軸はπ(ｘ)）
ｌｏｇ ｘは、自然対数の底ｅを底とする対数です。
ここでも、第１話で述べた物理学にとって重要な定数であるeが現れます。
素数とπ・eの間には、摩訶不思議な関係があることがガウス予想でも示唆されます。
それぞれをｘで割った存在確率π（ｘ）／ｘと１／ｌｏｇ ｘをグラフにしますと、
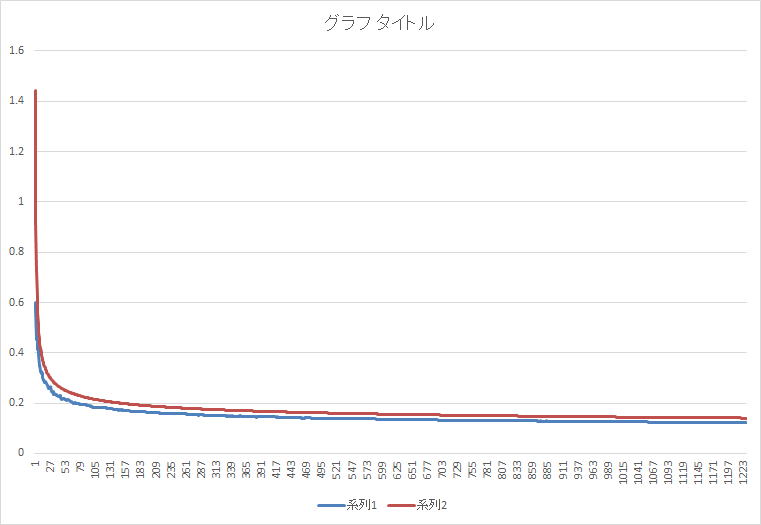
とても良い近似を示すことが分かります。
系列1がπ（ｘ）／ｘですし、系列２が１／ｌｏｇ ｘです。
素数を微少な局面で見ると規則性がまったく分からなかったのに対して、
大局で見ると見事な規則性があることが分かったわけです。
ガウス以前の研究が木を見ていたのに対して、
ガウスは森を見て素数の規則性を発見したのです。
さらに、ガウスは予想式を
π（ｘ）〜
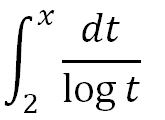に補正して精度を上げています。高校2年生で習う定積分ですね。
〜を＝に変更できれば、素数の規則性が発見されたことになります。
つまり、人類史上最大の難問が解決されたことになります。
ガウスの弟子であるリーマンは＝に変更するための大きな一歩を踏み出します。
次話のテーマである有名なリーマン予想です。
第１話へ 第３話へ
