第１話 オイラーの素数研究
このサイトの種々のプログラム入門講義を読んで頂けますと、
お分かりになりますように、私は素数に大きな魅了を感じています。
素数とは、
２，３，５，７，１１，１３，１７，１９，２３，・・・，
というように自分自身と１でしか割り切れない数のことです。
ただし、１は素数とは呼びませんので、
約数が２個である数が、素数であると定義してもよいことになります。
素数の間隔は、
・・・，９９０２３，９９０４１，９９０５３，・・・
だんだん大きくなる傾向がありますが、どこまでいっても、
・・・，９９９８９，９９９９１，・・・
と差が２しかない素数があったりします。
どう考えても素数は気まぐれにしか現れないように見えます。
果たして、素数には規則性があるのでしょうか。
数学者の中にも規則性はないと考えている人も大変多いのですが、
古代ギリシャ以来、規則性があるのではないかと多くの数学者が研究してきました。
人類史上最大の難問に最初の光明を与えた数学者は、オイラーです。
オイラーは、１７３５年に次の式を証明しました。
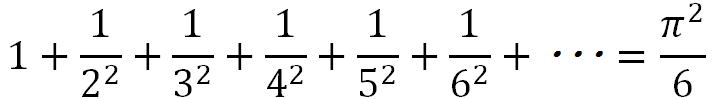
この式がどうして素数と関係があるのでしょうか。
実は、この式は、
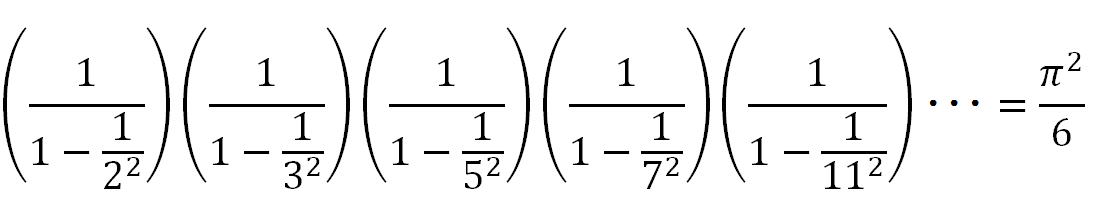
と同値なのです。
証明は、高校数学の範囲内で行えますので、難しいものではありません。
２番目の式の２乗になっている数
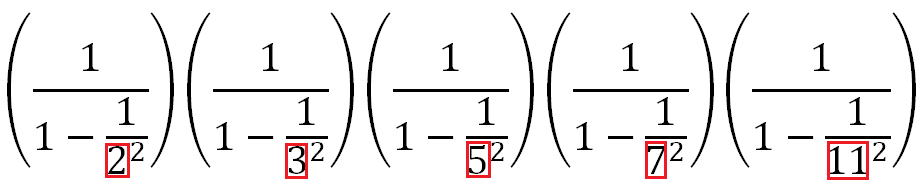
は、すべての素数です。
つまり、すべての素数からなる式を作ってみたら、
極限値はなんと
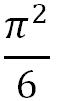であったのです。これは驚異的な事実です。
規則性がないように見えた素数から作った式が、なんと円周率と関係していたのです。
円周率πと自然対数の底eは、物質を究極まで突き詰めていくと、
いろいろな場面で現れる非常に重要な定数です。
物理学にとっては、なくてはならない定数なのです。
素数が不思議なことに、
宇宙の秘密を解き明かすときに重要なキーとなるπ
と関係していたのです。
オイラーは
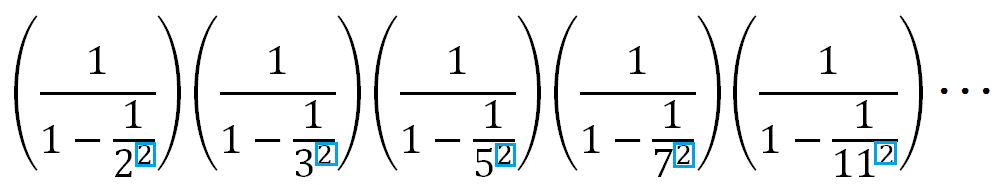
の２の部分を変数ｓに変えた関数をゼータ関数と呼び、
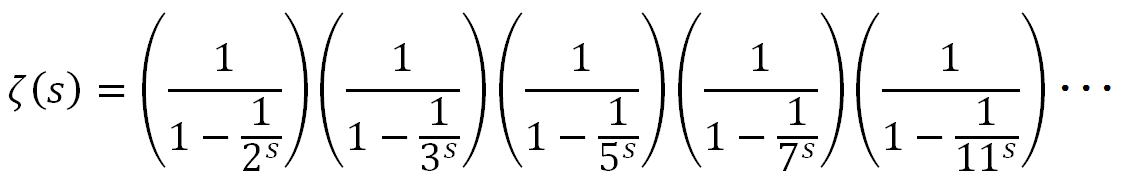
としました。
この記号を使いますと、先程の結論は、
ζ（２）＝
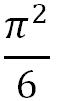となります。オイラーは、その他
ζ（４）、ζ（６）等も計算しており、
それぞれ
、
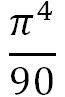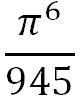になることを突きとめています。オイラーの研究によって、素数には規則性がある可能性が高まり、
数学者の素数研究は加速されることになります。
第２話へ
