第5話 10から19までの2乗計算規則と
21から99までの2乗計算規則の同一性の発見
NEKOははじめ嫌いであった先生が、
1学期期末テストごろになると一番のお気に入りの先生になっていました。
なぜかとても気が合うのです。
日常的に数学の先生と交流するようになっていました。
先生方の中では、もっとも親しく接するようになっていたのです。
そこで、友達に言っても取り合ってもらえなかった発見を先生に聞いてもらいました。
先生は、
『これは大変すばらしい発見だよ。ぜひ、研究を続けるように。
NEKOの発見は中学数学の範囲で証明できるから証明を試みてみな。
そして、2乗など特別な場合だけでなく、一般の場合で研究してみると良い。』
とNEKOにアドバイスしました。
NEKOは、
.gif)

 るんるんです。
るんるんです。
ニャオー、ニャオーです。
大好きな先生に褒められたのですから。
俄然やる気が出てきました。

2乗という特別の場合でない、2桁同士のかけ算の簡単な方法はないのだろうかと、
NEKOは、来る日も来る日も考えました。
計算規則の一般化を考えていました。
ですが、ヒントは特別な計算である2乗の計算の中に隠されているかもしれないと
NEKOは考え、2つの計算規則をもう一度見つめ直しました。
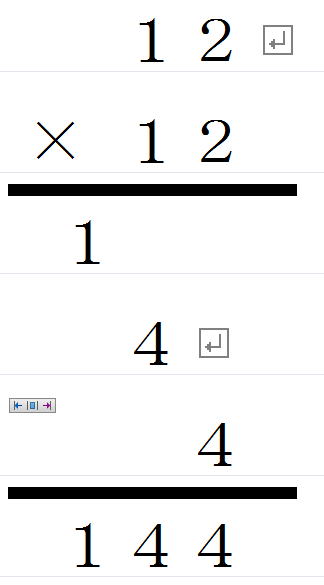
| 12×12は |
|
|
| 十の位の数字同士をかける |
|
1×1=1 |
| 一の位の数字同士を足す |
|
2+2=4 |
| 一の位の数字同士をかける |
|
2×2=4 |
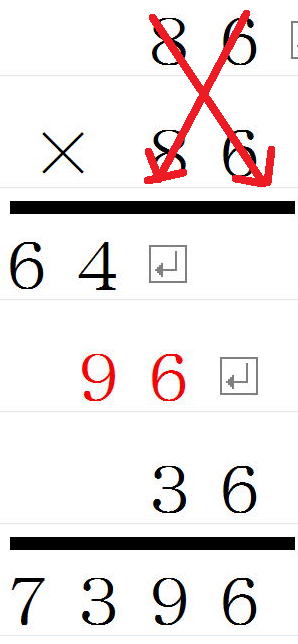
| 86×86は |
|
|
| 十の位の数字同士をかける |
|
8×8=64 |
| 十の位の数字と1の位の数字をかけて2倍する |
|
8×6×2=96 |
| 一の位の数字同士をかける |
|
6×6=36 |



この2つの図を見てNEKOの頭に電流が走りました。
両者を統一する道は、クロスだったのです。
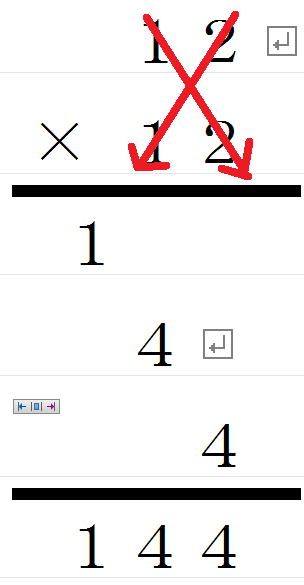
12×12の真ん中は一の位の数字の和2+2=4ではなく、
1×2+2×1=4ですし、
86×86の真ん中も8×6×2=96ではなく、
8×6+6×8=96なのです。
つまり、両方ともクロスにかけたものの和
(クロス和と呼ぶことにします。)だったのです。
まったく異なって見えた計算規則に中に、
本質的同一性が隠されていたのです。
さあ、いよいよ女子高生NEKOの大発見!
の大神髄であるリボン計算(リボン演算)は直前です。
第4話へ 第6話へ

初心者のためのjava 入門 基礎から応用まで
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第2部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座へ
VC++入門
VBA入門
専門用語なしのVBA入門
VB入門
初心者のためのEclipseによるJava入門





