第6話 画期的なリボン計算(リボン演算)の発見、
2乗だけでなく一般の2桁同士が第5話の計算方法でできる!
前話の発見、実はリボン計算(リボン演算)の発見に他なりません。
私(サイト運営者佐藤勝一)は、リボン計算(リボン演算)で
2桁の暗算ができたときは、
興奮しました
 。
。
私のぼんくらな頭では、
2桁同士のかけ算を暗算でやるなんて絶対に無理だったからです。
NEKOは第5話の発見をリボン計算(リボン演算)と名付けました。
驚くことに、リボン計算(リボン演算)は2乗という特殊な場合だけでなく、
一般の2桁同士のかけ算に適用できたのです。
これを発見したときにNEKOはどれだけ喜んだことでしょう。
NEKOにゃんにゃんです。

 にゃオーにゃオーです。
にゃオーにゃオーです。

本当にエキサイティングな出来事です。
特殊な場合の計算規則であると
思っていたリボン計算(リボン演算)が一般性を持っていたのです。
三平方の定理は、
最初直角二等辺三角形の場合で発見されたそうです。
きっと、ピタゴラス(人ではありません。グループです。)
も最初は直角二等辺三角形のみに成り立つ
特殊な定理にすぎないと思っていたはずです。
でも、ピタゴラスの誰かが一般の直角三角形になり立つことを
発見したときは、
NEKOと同じ気分

 にゃオーにゃオー、だったことでしょう。
にゃオーにゃオー、だったことでしょう。
実際にやってみましょう。
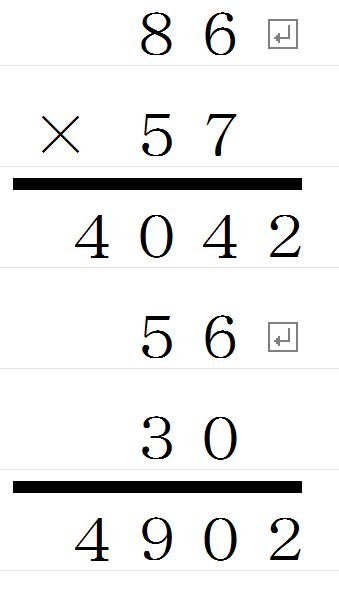
86×57は、次のように計算します。
| 86×57は |
|
|
| 十の位の数字同士をかける |
|
8×5=40 |
| 一の位の数字同士をかける |
|
6×7=42 |
| 右クロスをかける |
|
8×7=56 |
| 左クロスをかける |
|
6×5=30 |
| |
|
|
そして、4つの数字40、56、30、42を次のように配置して加えます。
なぜ、リボン計算(リボン演算)という名称でしょうか。

リボンにかけるからです。
いかなる場合もリボン計算(リボン演算)で計算できることを何例か示しましょう。



さらに暗算でやるためには、
クロス和を先に書いておいて
後で同位の数字同士をかけるようにした方が良いでしょうね。
つまり、

です。これなら2桁同士のかけ算の暗算ができます。
信じられないことです、
このコーナーをアップしてまだ半日もたっていないに
アクセス数は271に達しています。
私のサイトは、現在多いとき1万近くのアクセスがありますが、
新設のページは1日に数アクセスしかないのが普通です。
半日で271に達してしまったページは、
このホームページ始まって以来の事件です。
世の関心の高さを感じます。
第5話へ 第7話へ

初心者のためのjava 入門 基礎から応用まで
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第2部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座へ
VC++入門
VBA入門
専門用語なしのVBA入門
VB入門
初心者のためのEclipseによるJava入門







