第3話 1012×1012などの計算が暗算で計算できる!
やがて、NEKO は高校生になりました。
は高校生になりました。
そして、1学期の中間テスト以降に数学の習熟別の授業が始まりました。
このときから担当になった先生は、
とても怖い先生で、NEKOは自分の運命を呪いました。
怖いし、宿題は毎日たくさん出すので、
他のクラスの人たちをうらやましいと思いました。
ですが、この怖い先生との出会いがNEKOの人生を転回させていくことになるとは、
このときは夢にも思っていませんでした。
NEKOは計算法則の研究を続けました。
やはり、放課後1人しかいない教室で、
ガリレオになったのです。
チョークで黒板を埋め尽くしました。
余りに夢中になり、チョークをちょーくちょーく落としてしまいました。
NEKOはとてもおもしろい計算規則を発見しました。
NEKOは、教室に戻ってきた友達に早口で自分が見つけた計算法則を説明しました。
ですが、NEKOが余りに慌ただしく説明するので、
友達は理解できません。
そうです。
NEKOは、発見がうれしくて興奮して上手く説明できなかったのです。
それはそうです。
だって、1018×1018などが暗算でできてしまうのですから。
後に、友達はこう語りました。
黒板に数字がいっぱい書かれているだけで、
数学が苦手な私には、とても難しいと感じてしまうと。
やがて、友人たちもNEKOの発見の価値に気がつくことになるのですが。
さて、NEKOは何を発見したのでしょうか。
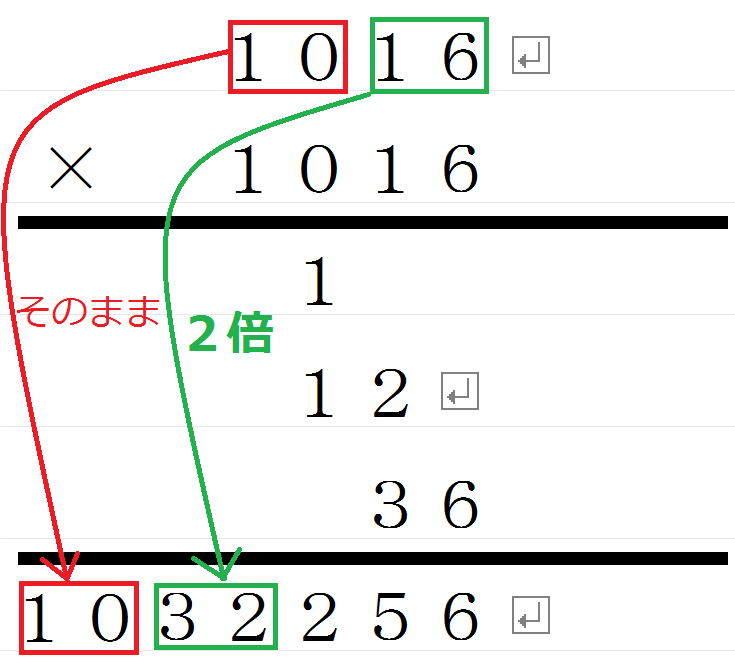
どうやって1012×1012を暗算で計算するのでしょうか。
まず、12×12を第1話の計算規則で計算します。
| 十の位の数字同士をかける |
|
1×1=1 |
| 一の位の数字同士を足す |
|
2+2=4 |
| 一の位の数字同士をかける |
|
2×2=4 |
| 答えは144 |
|
|
次に、1012の12だけ2倍にした1024をその144の右に添えるのです。
1024144です。
これが1012×1012の答えなのです。
NEKOはさまざまな例で、この法則が正しいことを検証しました。
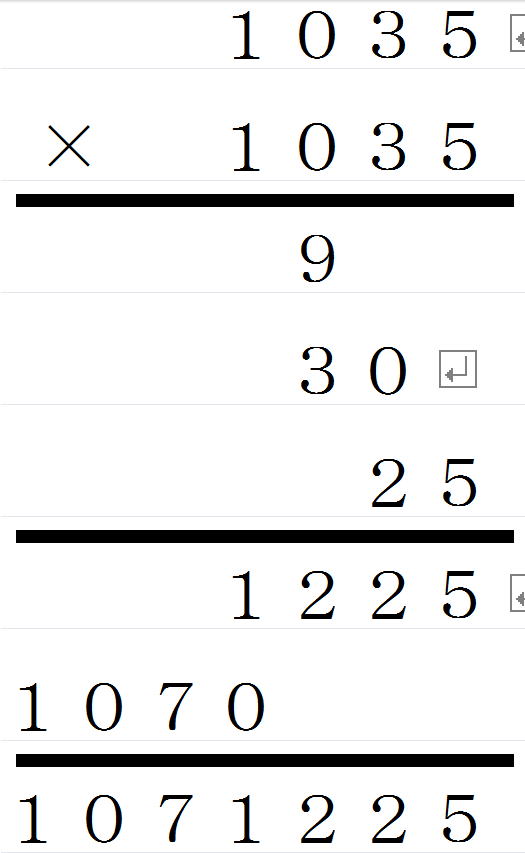
この場合は、35×35は第2話の計算規則
| 35×35は |
|
|
| 十の位の数字同士をかける |
|
3×3=9 |
| 十の位の数字と1の位の数字をかけて2倍する |
|
3×5×2=30 |
| 一の位の数字同士をかける |
|
5×5=25 |
によります。

NEKOは研究を続け、
3056×3056などにも一般化ができることを洞察します。
さらに、第1話の計算規則と第2話の計算規則が同じであることを発見します。
そして、それが2桁同士のかけ算の一般法則であることに気がつくのには、
それほど時間を要しませんでした。
そう革命的なリボン計算(リボン演算)の発見へと導かれていくのです。
第2話へ 第4話へ

初心者のためのjava 入門 基礎から応用まで
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第2部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座へ
VC++入門
VBA入門
専門用語なしのVBA入門
VB入門
初心者のためのEclipseによるJava入門
 は高校生になりました。
は高校生になりました。


