NEKO
 は自分の発見に興奮します。
は自分の発見に興奮します。きっと計算規則は、もっと拡張できる・・・
彼女は、1人残された放課後の教室でガリレオになります。
黒板に数字を書きまくり、
計算規則の拡張に奮闘しました。
次に考えた課題は、
86×86のような2乗の計算です。
最初に、女子中学生だったNEKOは10から19までの2乗の計算規則が
適用できないかと考えました。
第2話 21から99までの2乗計算規則の発見
NEKO は自分の発見に興奮します。
は自分の発見に興奮します。
きっと計算規則は、もっと拡張できる・・・
彼女は、1人残された放課後の教室でガリレオになります。
黒板に数字を書きまくり、
計算規則の拡張に奮闘しました。
次に考えた課題は、
86×86のような2乗の計算です。
最初に、女子中学生だったNEKOは10から19までの2乗の計算規則が
適用できないかと考えました。
| 86×86は | ||
| 十の位の数字同士をかける | 8×8=64 | |
| 一の位の数字同士を足す | 6+6=12 | |
| 一の位の数字同士をかける | 6×6=36 |
しかし、これは正解ではありません。
86の2乗は、7,396です。
黒板がチョークでいっぱいになりました。
ですが、今回の砦は、簡単には落城させることはできませんでした。
NEKOはあきらめません。
彼女の直感=直観が何かあるはずだと、
彼女に言い続けていたからです。
NEKOは、ふっと次のことに気がつきます。
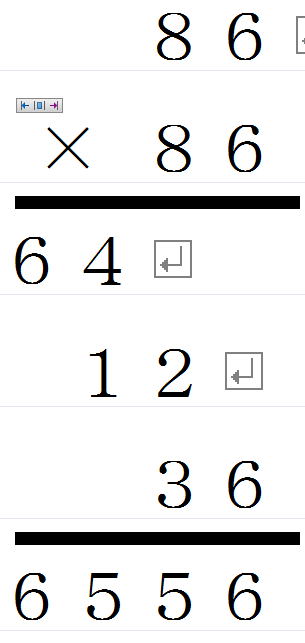
| 86×86は | ||
| 十の位の数字同士をかける | 8×8=64 | |
| 一の位の数字同士を足す | 6+6=12 | |
| 一の位の数字同士をかける | 6×6=36 |
一の位の数字同士を足す部分を
| 86×86は | ||
| 十の位の数字同士をかける | 8×8=64 | |
| 十の位の数字と1の位の数字をかけて2倍する | 8×6×2=96 | |
| 一の位の数字同士をかける | 6×6=36 |
と変更すると、

と正しい答えになることを。
偶然でしょうか。
NEKOはさまざまな問題例で検証を始めました。
| 47×47は | ||
| 十の位の数字同士をかける | 4×4=16 | |
| 十の位の数字と1の位の数字をかけて2倍する | 4×7×2=56 | |
| 一の位の数字同士をかける | 7×7=49 |

これを普通の筆算で確かめます。

正解です。
女子中学生は、『やった!これは間違いない。』と心の中で叫びました。
そして、何題も発見した計算規則で計算して、それを筆算で確かめました。
| 72×72は | ||
| 十の位の数字同士をかける | 7×7=49 | |
| 十の位の数字と1の位の数字をかけて2倍する | 7×2×2=28 | |
| 一の位の数字同士をかける | 2×2=4 |
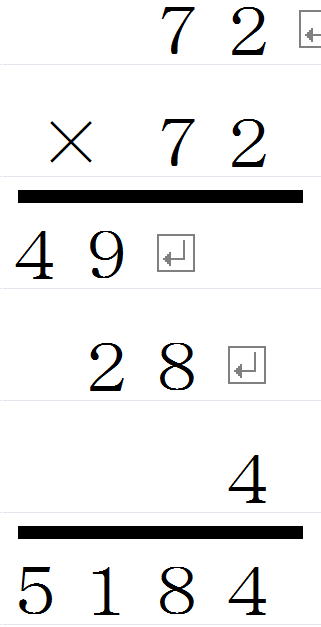
ピンポン!
| 35×35は | ||
| 十の位の数字同士をかける | 3×3=9 | |
| 十の位の数字と1の位の数字をかけて2倍する | 3×5×2=30 | |
| 一の位の数字同士をかける | 5×5=25 |

またまたドンぴっしゃり。
その後何題確かめても、すべてが正解でした。
NEKOは20から99までの
2乗の計算という難題を
攻め落とすことに成功したのです。
第1話へ 第3話へ

初心者のためのjava 入門 基礎から応用まで
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第2部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座へ
VC++入門
VBA入門
専門用語なしのVBA入門
VB入門
初心者のためのEclipseによるJava入門