①が一番難しい理由は、
当たりの判定が難しいということと、
さらに当たったらそのブロックを消さなければならないからです。
まず、当たり判定をするには、2つのことを考えなければなりません。
Ⅰ どのブロックが当たっているか?
Ⅱ ボールがどの範囲ならそのブロックと当たっていると判定するか。
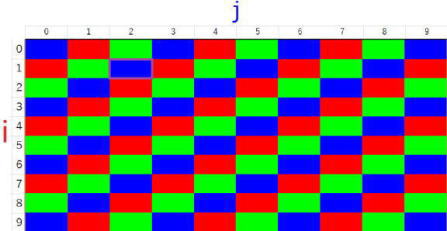
例えば、(2,1)(図の色と対応させてあります。つまり、(横、縦)になっています。)
ブロックの当たりの範囲は、
ボールの大きさまで考慮入れると、
どのようになるでしょうか。
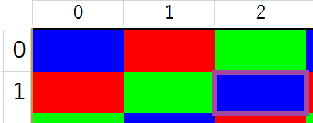
まず、(2,1)ブロックの4角の座標は、
(2×60,70+1×20)=(120,90)
((2+1)×60,70+1×20)=(180,90)
(2×60,70+(1+1)×20)=(120,110)
((2+1)×60,70+(1+1)×20)=(180,110)
式が?の方は、図から考えて下さい。
図を見れば明らかなのに、わざわざ複雑な式を入れているのは、
一般化できなければ、汎用性=普遍性のあるプログラムを組みことができないからです。
そこに半径10のボールの大きさを考慮に入れると、

円の中心の限界は
上から時計回りに、
(120,80)、(180,80)、(190,90)、(190,90)、
(190,110)、(180,120)、(120,120)、(110,110)
となります。
(j,i)ブロックと一般化すると、
先ほどの式は
(j×60,70+i×20)
((j+1)×60,70+i×20)
(j×60,70+(i+1)×20)
((j+1)×60,70+(i+1)×20)
すなわち、
(60*j,70+20*i)
(60*(j+1),70+20*i)
(60*j,70+20*(i+1))
(60*(j+1),70+20*(i+1))
ですから、
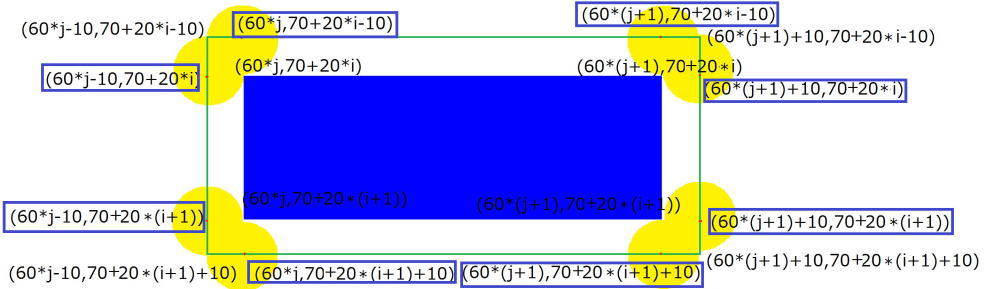
円の中心の限界は、
やはり時計回りに、
(60*j,70+20*i-10)、(60*(j+1),70+20*i-10)、
(60*(j+1)+10,70+20*i)、(60*(j+1)+10,70+20*(i+1))、
(60*(j+1),70+20*(i+1)+10)、(60*j,70+20*(i+1)+10)、
(60*j-10,70+20*(i+1))、(60*j-10,70+20*i)
ということになります。
1行目は上からぶつかる場合、
2行目は右からぶつかる場合、
3行目は下からぶつかる場合、
4行目は左からぶつかる場合になります。
ですから、細かく分けるとif文は4種類になります。
大きく分ければ上下と左右ということになります。
そして、どんな速さにも対応できるようにするためには、
範囲の幅は10程度は必要でしょう。
もし、10の幅で通り抜けてしまう場合には、
もう少し幅を取ります。
最終的にチューイングをして、
試行錯誤が必要になります。
第3話へ 第5話へ
第2部目次に戻る 第1部目次に戻る
初心者のための excel 2016 マクロ VBA 入門講義 基礎から応用まで
vc++ c言語 c++ 入門 初心者 基礎から応用まで
ecliqse c++ 入門
魔方陣 数独で学ぶ VBA 入門
数独のシンプルな解き方・簡単な解法の研究
VB講義へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための世界で一番わかりやすいVBA入門講義(基礎から応用まで)
初心者のための VC++による C言語 C++ 入門 基礎から応用まで第1部
ecliqse java 入門
java 入門 サイト 基礎から応用まで
本サイトトップへ