第1話 引き算の規則
n進数の引き算は、
10進数と同じく、小さい方から大きい方を引いたときには、
負の数になります。
足し算のときと同じで、
配列
int d[10000],e[10000];
を用意しておき、大きい方をdに小さい方をeに代入するようにして、
もし、b[i]の方が大きいときには、
先頭に-を付けることにします。
ですから、これからは大きい方から小さい方を引くという条件下で考えます。
この仮定のものとでは、
2進数の引き算規則は
10-1=1
1-0=0
1-1=0
0-0=0
のみとなります。
3進数なら
10-1=2
等です。
例えば、2進数の引き算
101(2)-11(2)
を計算してみますと、
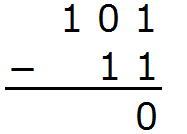
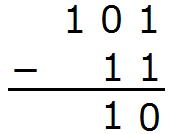
では、もう少し複雑な例を出しましょう。
101101(2)-11011(2)

1-1から0です。
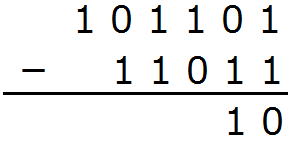
0から引けないので10-1=1
1つ上の位は0になっています。
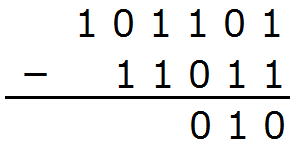
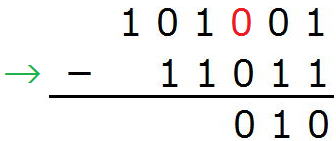
すでに1は0になっていますから、
0-0で0となります。

1-1から0です。
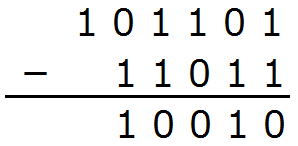
最後は10-1=1
です。
以上で計算終了です。
次は,5進数をやってみましょう。
321404(5)-43021(5)
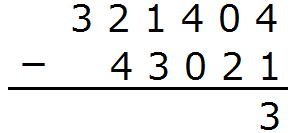
4-1から3です。
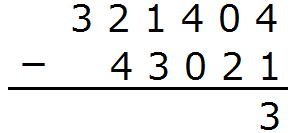
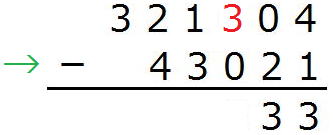
0から2は引きないので、上から1つ借りてきて
10(5)-2(5)=(1×5+0)-2=3です。
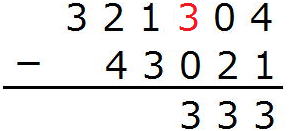
1つ貸したので3-0=3です。
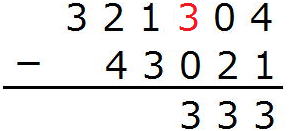
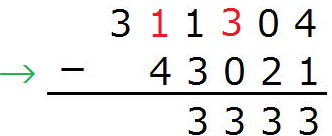
1から3は引けないので、上から1つ借りてきて
11(5)-3(5)=(1×5+1)-3=3です。

1つ下に貸してしまったので、
1-4ですがこれも引けないので、
上から1つ借りてきて、
11(5)-4(5)=(1×5+1)-4=2です。

最後は1つ貸してしまったので3→2となっています。
それでは、皆さん
次の引き算を実行してください。
① 101011(2)-11101(2)
② 21021(3)-201(3)
③ 430213(5)-34201(5)
④ 6543210(7)-5646634(7)
⑤ 325647(8)-23667(8)
プログラミングにおいては、敵を知ることが必要です。
手で計算して、対戦相手の本質を知って、
初めて攻略できます。
