第25講 ｎ進数の演算－－－その１ 加法
第12話 プログラム解説その６
プログラム主要再掲
int g(int* a,int* b,int* c,int n){
int i,j,k,d[10000],e[10000];
for(i=0;;i++){
if(a[i]==n){
j=i;
break;
}
}
for(i=0;;i++){
if(b[i]==n){
k=i;
break;
}
}
if(j>=k){
for(i=0;i<=j+2;i++){
c[i]=0;
d[i]=0;
e[i]=0;
}
for(i=0;i<j;i++)d[i]=a[i];
for(i=0;i<k;i++)e[i]=b[i];
for(i=0;i<j;i++){
c[i]+=(d[i]+e[i]);
c[i+1]+=c[i]/n;
c[i]=c[i]%n;
}
for(i=j+2;;i--){
if(c[i]>0){
c[i+1]=n;
return(i+1);
}
}
}
else{
for(i=0;i<=k+2;i++){
c[i]=0;
d[i]=0;
e[i]=0;
}
for(i=0;i<k;i++)d[i]=b[i];
for(i=0;i<j;i++)e[i]=a[i];
for(i=0;i<k;i++){
c[i]+=(d[i]+e[i]);
c[i+1]+=c[i]/n;
c[i]=c[i]%n;
}
for(i=k+2;;i--){
if(c[i]>0){
c[i+1]=n;
return(i+1);
}
}
}
}
いよいよ
for(i=j+2;;i--){
if(c[i]>0){
c[i+1]=n;
return(i+1);
}
}
を説明して解説は終わりになります。
この部分は、c[i]に終わりの記号nを入力することを任務にしています。
前回までの計算で
０４２４２
と計算されています。つまり、
c[0]=2,c[1]=4,c[2]=2,c[3]=4,c[4]=0
となっています。
初期化によって最初に０がはいっていたことも考慮に入れると、
０００４２４２
と計算されています。つまり、
c[0]=2,c[1]=4,c[2]=2,c[3]=4,c[4]=0,c[5]=0,c[6]=0
です。
どうして、最後が6と申しますと、
| 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| ０ | ０ | ０ | ４ | ２ | ４ | ２ |
この表からｊ=4であり、j+2は6になるからです。
繰り上がりがある場合も考えても、
やはり
for(i=j+1;;i--){
if(c[i]>0){
c[i+1]=n;
return(i+1);
}
}
| 5 | 4 | 3 | 2 | 1 | 0 |
| ０ | ０ | ４ | ２ | ４ | ２ |
で十分であったようです。
私も皆さんと一緒に試行錯誤をしながら進めていますから、
ミスは結構多いと思います。
最後の結果だけ示すという講義方法もあるかと思いますが、
思考過程も示した方が、
講師役の私も迷いながら、
進めていることが分かり安心するのではないでしょうか。
for(i=j+1;;i--){
if(c[i]>0){
c[i+1]=n;
return(i+1);
}
}
| 5 | 4 | 3 | 2 | 1 | 0 |
| ０ | ０ | ４ | ２ | ４ | ２ |
の２つを見れば、意味がお分かりかと思います。
添え字の5から始めて、始めて０以外の数字の出てくる、
添え字の１つ手前に終わりの印n（今の例では５）を入力しているのです。
| 5 | 4 | 3 | 2 | 1 | 0 |
| ０ | ５ | ４ | ２ | ４ | ２ |
これで後は表示関数にかければ、正しい計算結果が出力されます。
難解ですよね。
実は、引き算→かけ算→割り算と進むとより問題難度が上がります。
ですが、皆さん粘り強く挑戦しましょう。
私は、これに平方根の計算・素数判定システム・因数分解システムも加えましたが、
有に２ヶ月がかかったのです。
割り算まででも１ヶ月はかかっています。
時間をかけるのは、それに見合う見返りが十分にあると考えているからです。
私には才能がありませんので、
無理ですが、才能のある皆さんが研究していけば、
人類史上に時期を画す研究結果を残せるのではないでしょうか。
第26講では、引き算を考えます。
ですが、第25講の最後の課題として
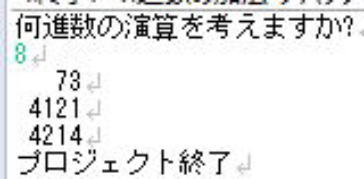
等の計算が合っているかを10進数に翻訳して、
10進数の和と比較することによって確かめる検算をすることにしましょう。
