第１話 ポインタとは？
（この話は、本サイトの小学生からエンジニアまでのC言語入門第７講第１話を少し改良して、
流用しています。)
ポインタは、C++を魅惑的なものにしていると同時に、
初心者にとって大きな壁でもあります。
ポインタとは、簡単にいうと、
『箱の住所を代入できる箱』
です。
えっ？！
そんなこといわれるとますます謎めいていますね。
もう少し正確にいうと、
『変数のアドレスを納める変数』
です。
ますます謎めいています。
いままで変数を箱と比喩してきました。
ですが、正確にいうとデータを収めるメモリです。
メモリ(メモリーと書くこともあります）とは記憶装置のことです。
記憶装置には、ハーディスクや半導体メモリなどがありますが、
いずれにしろ記憶装置のある場所をデータを収納する場所として指定しています。
記憶装置の場所をアドレス（住所）といいます。
変数型（データ型）によって、
１つの変数に割り当てられる場所の大きさは異なってきますが、
データ型の容量の大きさに従った幅でメモリ
（この場合は記憶装置ではなく記憶容量
メモリは記憶装置という意味と記憶容量という意味があります。
さらに、記憶媒体つまり記憶を載せるものという意味もあります。
記憶媒体という表現がわかりにくいと思いますが、
例えば、皆さんが授業中に書くノートも記憶媒体の1つです。
記録を載せておくもの＝記憶を書いておくものが記憶媒体です。
記憶媒体のことをメディアともいいます。
マス・メディアは巨大な記憶媒体の意味です。）
が割り振られます。
例えば、int型であれば4バイト（メモリ＝記憶容量の単位）の記憶容量がありますので、
int a;
であれば、aの記憶の場所として1000〜1003
（うっかりするとそれでは3バイト分しかないと考えてしまいますが、
1000,1001,1002,1003で4バイト分ですよ。
ですが、1000〜1004と表記することもあります。
このときは1001以上1004以下を表しています。
ですから、1001,1002,1003,1004が対象範囲です。
ポインタが収納するアドレスは、
対象範囲1001,1002,1003,1004の1つ手前のアドレス1000です。
ですから、1000〜1004の表記となります。）
までが割り振られます。
メモリ（記憶媒体＝記憶するもの）には番地があり、
それが数字（正確には16進数表示）で示されています。
つまり、メモリ（記憶媒体）の場所を数字による番地で示しているのです。
説明の補足のために
VC++ C言語 C++ 入門 初心者 基礎から応用まで
の該当部分をそのまま引用します。
変数iとは何でしょうか。
今まで箱のイメージで説明してきましたが、
正確に言うと、メモリの番地が割り当てられている、のです。
int ｉ；と宣言し場合、
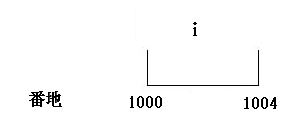
例えば、メモリーの番地の1001から1004をiのメモリー領域にあてるのです。
int型は、4バイトなので4飛びになっています。
char i;と宣言した場合は、char型は1バイトなので
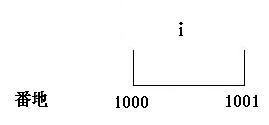となります。double i;なら8バイトで
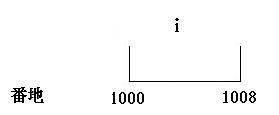となります。この引用では
は1001以上1004未満を表しています。もし、メモリの住所である1000（これは対象範囲の1つ手前のアドレス）等を収納できる箱（変数）があったら・・・
実は、とても便利なのです。
『コンピュータの仕組みに応じたプログラミングが出来る!』
出来ることがC言語の魅力だといいましたが、
このポインタ（変数の住所を収納する変数）こそが
その芸当が出来る最大の理由です。
どうしてですか。
プログラムって結局箱（変数）と社員（関数）から出来ています。
そして、変数にも関数にもアドレスがあるのです。
つまり、どの変数にもどの関数にも踊る舞台が指定されているのです。
A市民会館小ホール１におけるステージの一番前の一番左側のように。
変数や関数が活躍する場所を知って、
コントロールできたら、とても大きいのです。
それぞれの役者（変数や関数）がどこで仕事をしているのかを知っていれば、
その役者の監督であるプログラマーにとってどれだけ仕事がしやすいでしょうか。
メモリ（記憶媒体）のアドレスを管理することによって、
変数や関数を自由に操れる！
のです。
プログラマーの動かす駒がどこにあるか、
それを知っていればこれほど強力なことはありませんね。
変数や関数のアドレスを収納する箱（変数）をポインタというのです。
謎めいた『変数のアドレスを納める変数』の意味が少しは分かったのではありませんか。
でも、まだまだよく分からない・・・ですね。
当然です。
原理をいくら詳しく説明されても、
人間は納得できないものです。
納得できるためには、
実際にポインタを操作することが必要です。
プログラミングには、
習うより慣れろ!
の部分があるのです。
もっとも数学をはじめてして、どの学問分野にもいえることですけどね。
具体的な話を第２話以降でしていくことにしましょう。
