第２講変数第４話実数型変数

第２講変数
第４話実数型変数
整数型と文字型を学びましたので、
さらに、実数型を加えましょう。
コードを次のように変更しましょう。

#include<stdio.h> //C言語プログラミングをはじめるためのお呪い。
int main() {
　　int a; //整数を入れる箱aを用意
　　char b; //文字を入れる箱bを用意
　　float c; //小数を入れる箱cを用意
　　printf("はじめてのC言語プログラミング体験\n");
　　printf("まず、変数から学ぼう！\n");
　　a = 2; //箱aに2を入れた
　　printf("%d\n", a); //箱aの中身を表示
　　b = 'a';
　　printf("%c\n", b); //箱bの中身を表示
　　c = 3.14;
　　printf("%f\n", c); //箱cの中身を表示
　　return(0); //mainを閉じるためのお呪い。
}

実行結果

　　float c; //小数を入れる箱cを用意
注釈文ではわかりやすく小数と解説していますが、
正確には実数型変数の宣言といいます。
表示が3.14000となっていますが、
表示を
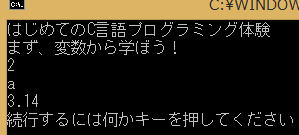3.14としたいときには、
　　printf("%f\n", c); //箱cの中身を表示
を
　　printf("%.2f\n", c); //箱cの中身を表示
とします。.2は小数以下第２位までの表示を意味します。

さて、コードを次のように変更して
実行してください。
#include<stdio.h> //C言語プログラミングをはじめるためのお呪い。
int main() {
　　int a; //整数を入れる箱aを用意
　　char b; //文字を入れる箱bを用意
　　float c; //小数を入れる箱cを用意
　　printf("はじめてのC言語プログラミング体験\n");
　　printf("まず、変数から学ぼう！\n");
　　a = 2; //箱aに2を入れた
　　printf("%d\n", a); //箱aの中身を表示
　　b = 'a';
　　printf("%c\n", b); //箱bの中身を表示
　　c = 3.1415926535;
　　printf("%.10f\n", c); //箱cの中身を表示
　　return(0); //mainを閉じるためのお呪い。
}
.10となっていますから、3.1415926535と表示されるはずですが、
実行画面は残念ながら、

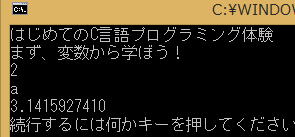
と3.1415927410となっています。
わかりやすく並べると
3.1415926535
3.1415927410
と小数第６位までしか正確に表示されていません。
float型は小数第６位が限界だからです。
では、第10位まで表示させるにはどうしたらよいか。
　　float c; //小数を入れる箱cを用意
を
　　double c; //小数を入れる箱cを用意
と変更すれば良いのです。
変更すると、

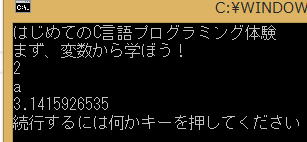
と正確に表示されました。

doubleで宣言された変数を倍精度実数型変数といいます。
ならば、大は小を兼ねるということで
いつでもdouble型で宣言すれば良さそうなものですね。
ですが、小数第６位までということがわかっているときには、
float型で宣言すべきです。
理由は、double型はメモリが２倍食い実行速度が遅くなるからです。
今扱っているプログラムでは、問題ありませんが、
将来は円周率を何万桁も計算させたり、
1937桁の完全数
（自分自身を除く約数の和が自分自身と一致する数、
例２８　１＋２＋４＋７＋１４＝２８)
を求めたりしますが、このときななるべくメモリ容量の小さい変数型を利用した方が良いのです。
メモリ容量と計算速度は反比例するからです。
因みに1937桁の完全数を示しておくと、

33570832131986724437010877211080384841138028499879725454996241573482158450444042882048778
80943769038844953577426084988557369475990617384115743842473013080704762365594223617485050

91085378276585906423254824947614731965790746560999186007644047021816602944691217787379658
22199901663478093006075022359223201849985636144177185925402078185073015045097727084859464
74363553778150028491588024488630646178598295607206001347495561785148168018598855713660922
48418178770836089511911231748852264161306831977106673923510073745037554033525314762279435
90071651702697594241031955529898971218001214641774673134944471562560957179657881556419122
10293545029975181334051517095616795109545364948557615066010168916065801177019327422630828
05077868350495491125766545101196704567459398901942052551753844844899093289676469881631559
82471564998196261632751283127879509198074253193409580454562488664383465379885002735506153
98885150664513775927555398821942543976473239982471243812505411752383743825674443705501944
10510064899723416091179784045637949920048730575184557487014449512383771396204942879824895
29827233140637014837408856156199515457669607964052126908149265601786094447595560440059050
09176354711409225537139742580786755435211254219478481549478427620117084594927467463298521
04210755317849183589266903954636497214522654057134843880439116344854323586388066453138262
06591131266232422007835577345584225720310518698143376736219283021119287617896146885584860
06504887631570108879621959364082631162227332803560330947564239080449946015679785536101824
66961012539222545672409083153854682409318461669624959834076071416012518895444070088158747

44654769507268678051757746956891212485456261121386667407711139619071530923355823178662705
37439303504902260388247974233479940713028014876929859774377819305034874974078692809603390
62959101992381813385578569781918606472562097081682291161563009780591970268557268776497670
72684960463452763160384093838292277544911857859658328888332628525056

（http://goodboone.com/izime/science/entry1247.htmlより引用)
となります。
これが現時点で私の見つけた最大の完全数です。
実験を２時間程度でやめてしまいましたので最高記録は1937桁ですが、
おそらく半日も計算させると2663桁までの完全数が表示されることでしょう。
ですが、その次の5834桁は残念ながら５日以内では出てこないでしょうね。
5834桁を半日程度で計算させるためには、
今の最速のプログラムをさらに改良する必要があります。
因みに人類の最高記録は、５千万桁ぐらいです。
一般家庭の800台を並列に走らせて作った世界記録です。
その前の２千万桁ぐらいは世界中のコンピュータを並列に走らせた作った記録だそうですから、
800台のコンピュータで５千万桁の完全数を見つけたということは、
プログラムの大幅にして根本的な改善があったのでしょうね。
２つの記録は同じチームが達成しています。

素数や完全数なんて興味がないと思う方もいらっしゃるかもしれませんが、
素数なしには最先端物理学（超弦理論）も成立しませんし、
IT社会や現代金融資本主義の成立もないのです。
素数を応用したRSA暗号理論のお陰で、スマホやコンピュータが安心して使えるし、
軍事機密や企業機密が守れるのです。
現代社会を支えている基盤は素数などを研究する整数論なのです。

第３話へ　第５話へ
　

初心者のための excel 2016 マクロ VBA 入門講義基礎から応用まで
 vc++ c言語 c++ 入門初心者基礎から応用まで
 eclipse c++ 入門
魔方陣数独で学ぶ VBA 入門
数独のシンプルな解き方・簡単な解法の研究
VB講義へ
 ＶＢ講義基礎へ
 初心者のための世界で一番わかりやすいVisual C++入門基礎講座
 初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
 初心者のための世界で一番わかりやすいVBA入門講義（基礎から応用まで）
初心者のための VC++による C言語 C++ 入門基礎から応用まで第１部
eclipse java 入門
 java 入門サイト基礎から応用まで
本サイトトップへ