3*(i/3)+(j/3)ていったい何なんでしょうか。
ここでの課題は、
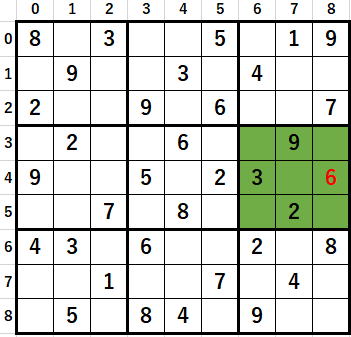
座標(4,8)からいかにして、
ブロック番号
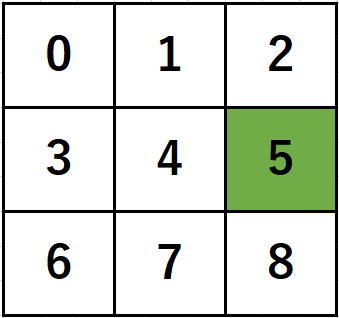
5を作り出すかです。
3*(i/3)+(j/3)に(4,8)を代入すると、
3*(i/3)+(j/3)=3*(4/3)+(8/3)=3*1+2=5
で確かに5を作れています。
iもjもint型ですから、i/3=4/3=1と小数部分が切り捨てられ、
整数に丸められるのでしたね。
でも、??というところでしょう。
3*(i/3)では何をしているかと申しますと、
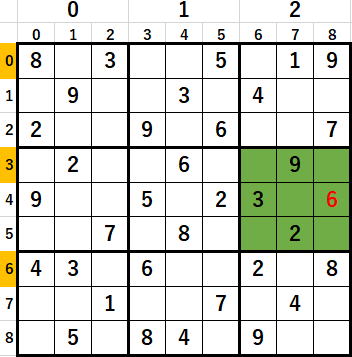
0,1,2はすべて0
3,4,5はすべて3
6,7,8はすべて6にしています。
i/3で小数部分を切り捨てて、
3倍しているので、
ブロックの先頭番号を取得できるのです。
また、(j/3)では、

0,1,2はすべて0
3,4,5はすべて1
6,7,8はすべて2にしています。
3で割ったときの商ですから当然そうですよね。
ということは、
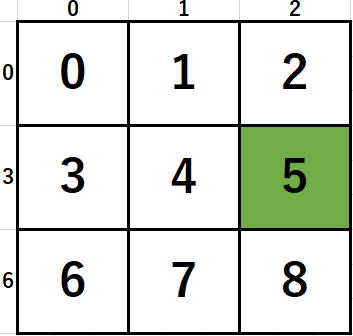
3*(i/3)と(j/3)の合計3*(i/3)+(j/3)は、
ブロック番号になりますね。
実際すべて縦と横を足してみると、
0+0=0,0+1=1,0+2=2,
3+0=3,3+1=4,3+2=5,
6+0=6,6+1=7,6+2=8
で見事にブロック番号を作り出しています。
y座標(縦座標)iとx座標(横座標)jから、
ブロック番号を作り出す3*(i/3)+(j/3)という手法を
是非頭に強く刻み込んでください。
数独(ナンプレ)問題自動生成アプリを開発する際に、
しばしば使います。
各行に対応する配列
int gy[8][8];
各列に対応する配列
int rt[8][8];
各行に対応する配列
int br[8][8];
を用意して、白を1、色を0と定義すると、
セルに入力できる条件は、
(i,j)に5を入力する場合には、
if (gy[i][4]*rt[j][4]*br[3*(i/3)+(j/3)][4]==1){
とすればよいのです。
1つでも、条件不可だと入れられませんね。
3つとも1であることを確認する方法として、是非とも、
gy[i][4]*rt[j][4]*br[3*(i/3)+(j/3)][4]==1
かけ算を使用する方法があることを頭に入れてください。
第7話へ 第9話へ
