各行・各列・各ブロックに、
１，２，３，４，５，６，７，８，９
の数字が漏れなく１つずつ入る・・・
ようにするということは、
重複なしに入るようにするということです。
重複なしにするために、
第３話から第５話までは、
for文を使って重複を調べました。
でももっと簡単にできる方法があります。
私は、その方法を色塗りのイメージで説明します。
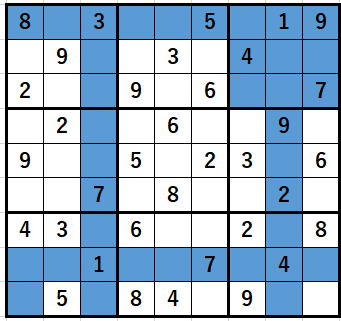
薄い青で塗ってあるところは、
１を入れることの出来ないます（セル）です。
ますのことをこれからはセルと呼びます。
白いセルのみが入力可能です。
１から９までのそれぞれの数字に対応する色があり、
それぞれの色が塗られているとイメージしてください。
同じ紙にいろいろな色を塗ってしまったのでは、
色が混ざってしまいますから、
数独（ナンプレ）の１つの問題について、同じ紙が９枚あり、
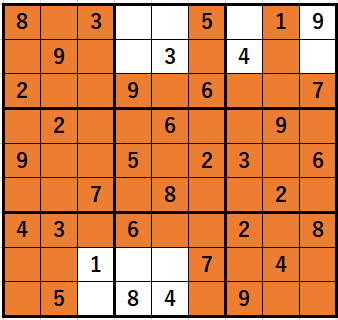（オレンジは、2の入れられない場所）のように、
それぞれの数字に対応する色が塗られているとイメージするのです。
そして、例えば、
塗られていない状態（白）を1と定義し、
塗られている場合には、0と定義して、
1のとき、すなわち白のときのみに入れていくということです。
どうして、Ver.1が完成しているのに改良するのか？
それは、今示したオレンジの図の１番左で、１番下のブロックを見れば分かります。
白いセルが１つしかありません。
そうです。2の入る場所が確定しているのです。
1の下、5の右隣です。
同じ行や列に同じ数字を入れられないことを、
私はライン排除と呼びますが、
数独（ナンプレ）を仮定法を使わずに理詰めで解く際に、
ライン排除による確定は、もっとも頻繁に使う方法です。
ライン排除によって確定することをライン排除確定と呼びますが、
色塗りの方法は、
ライン排除確定やこの後に説明する１：１対応確定などの原理にも使える、
優れものなのです。
理詰めで解く＝仮定法を使わない＝仮置き法を使わない方法を、
私は確定法と呼んでいます。
確定法で数独（ナンプレ）を解いたり、
確定法でのみで解ける数独（ナンプレ）の問題を生成するのに、
色塗りの方法は、絶対に不可欠です。
具体的には、
各行に対応する配列
int gy[8][8];
各列に対応する配列
int rt[8][8];
各行に対応する配列
int br[8][8];
を用意しておいて、最初はすべて1に初期化しておいて、
例えば、セル(i,j)に3が入力された場合には、
gy[i][2]=0;
rt[j][2]=0;
br[3*(i/3)+(j/3)][2]=0;
（2は3-1です。）とするのです。
gy[i][2]=0; はi行目に3
（2は3-1です。添え字は0から始まりますから、
いつでも1つずれるのでしたね。）
に対応する色が塗られたと考えてください。
rt[j][2]=0; はj列目に3
に対応する色が塗られた・・・
br[3*(i/3)+(j/3)][2] は3*(i/3)+(j/3)ブロックに、に3
に対応する色が塗られた・・・
3*(i/3)+(j/3)の意味が分からない！！！
私も、大変混乱しました。
第６話へ 第８話へ
