第16講 全セルリスト構造解析(全体リスト構造解析)によって数独(ナンプレ)を解く
第2話 セル(1,2)のリスト構造
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
|
|
|
4 |
9 |
|
|
|
|
| 1 |
9 |
|
|
|
|
3 |
|
|
|
| 2 |
|
1 |
|
|
|
|
6 |
8 |
|
| 3 |
|
|
3 |
8 |
|
|
|
1 |
2 |
| 4 |
|
|
|
|
|
|
|
|
|
| 5 |
6 |
7 |
|
|
|
4 |
3 |
|
|
| 6 |
|
6 |
7 |
|
|
|
|
4 |
|
| 7 |
|
|
|
3 |
|
|
|
|
1 |
| 8 |
|
|
|
|
5 |
7 |
|
|
|
まず、行の条件から、
9と3が候補から外されます。
次に、列の条件から、
さらに、7が候補から外されます。
最後に、ブロックの条件から、
1が候補から外されます。
結局残った数字は、小さい順に
2,4,5,6,8
の5つです。この5つが、
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
|
|
|
4 |
9 |
|
|
|
|
| 1 |
9 |
|
|
|
|
3 |
|
|
|
| 2 |
|
1 |
|
|
|
|
6 |
8 |
|
| 3 |
|
|
3 |
8 |
|
|
|
1 |
2 |
| 4 |
|
|
|
|
|
|
|
|
|
| 5 |
6 |
7 |
|
|
|
4 |
3 |
|
|
| 6 |
|
6 |
7 |
|
|
|
|
4 |
|
| 7 |
|
|
|
3 |
|
|
|
|
1 |
| 8 |
|
|
|
|
5 |
7 |
|
|
|
の
に入る候補の数字です。
第16講第1話から読み始めた人のために、
解説しておきますと、
候補のことをリストと呼び、
そのリストの集合{2,4,5,6,8}
とリスト数(集合の要素数)5個をセル(1,2)のリスト構造と呼んでいるのです。
普通集合{2,4,5,6,8}の中に集合の要素個数5個は概念として含まれていますから、
リスト構造は{2,4,5,6,8}であるといえば済む話なのですが、
わざわざリスト構造を {2,4,5,6,8}と5個 と呼んでいる理由につきましては、
以下の説明の後説明します。
要素個数を配列mx(1,2)、リストの集合を配列
lst(1,2,k)で表すことにしますと、
結局、セル(1,2)のリスト構造は以下のようになります。
lst(1,2,0)=2
lst(1,2,1)=4
lst(1,2,2)=5
lst(1,2,3)=6
lst(1,2,4)=8
mx(1,2)=5
配列の添え字が0から始まるため、
最後のリストlst(1,2,4)=8
の添え字4は
mx(1,2)-1と等しくなります。
では、皆さん次の課題です。
最初、
lst(1,2,0)=1
lst(1,2,1)=2
lst(1,2,2)=3
lst(1,2,3)=4
lst(1,2,4)=5
lst(1,2,5)=6
lst(1,2,6)=7
lst(1,2,7)=8
lst(1,2,8)=9
mx(1,2)=9
と初期化しておいてから、
セル(1,2)のリスト構造解析を行って、
lst(1,2,0)=2
lst(1,2,1)=4
lst(1,2,2)=5
lst(1,2,3)=6
lst(1,2,4)=8
lst(1,2,5)=1
lst(1,2,6)=3
lst(1,2,7)=7
lst(1,2,8)=9
mx(1,2)=5
と変更するプログラミングを考えて下さい。
このプログラミングの注目すべき点は、
lst(1,2,5)=1
lst(1,2,6)=3
lst(1,2,7)=7
lst(1,2,8)=9
と候補から外された数字も一応リストに残しておくことです。
理由は、試行錯誤で
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
|
|
|
4 |
9 |
|
|
|
|
| 1 |
9 |
|
|
|
|
3 |
|
|
|
| 2 |
|
1 |
|
|
|
|
6 |
8 |
|
| 3 |
|
|
3 |
8 |
|
|
|
1 |
2 |
| 4 |
|
|
|
|
|
|
|
|
|
| 5 |
6 |
7 |
|
|
|
4 |
3 |
|
|
| 6 |
|
6 |
7 |
|
|
|
|
4 |
|
| 7 |
|
|
|
3 |
|
|
|
|
1 |
| 8 |
|
|
|
|
5 |
7 |
|
|
|
空いているセル(升)に数字を入れていくわけですが、
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
2 |
|
|
4 |
9 |
|
|
|
|
| 1 |
9 |
|
|
|
|
3 |
|
|
|
| 2 |
|
1 |
|
|
|
|
6 |
8 |
|
| 3 |
|
|
3 |
8 |
|
|
|
1 |
2 |
| 4 |
|
|
|
|
|
|
|
|
|
| 5 |
6 |
7 |
|
|
|
4 |
3 |
|
|
| 6 |
|
6 |
7 |
|
|
|
|
4 |
|
| 7 |
|
|
|
3 |
|
|
|
|
1 |
| 8 |
|
|
|
|
5 |
7 |
|
|
|
入れた数字によって、リスト構造が
lst(1,2,0)=4
lst(1,2,1)=5
lst(1,2,2)=6
lst(1,2,3)=8
lst(1,2,4)=1
lst(1,2,5)=2
lst(1,2,6)=3
lst(1,2,7)=7
lst(1,2,8)=9
mx(1,2)=4
(紺がセル(1,2)の候補の数字、
そして、2が候補から外されてしまった数字)
と変化するわけですが、
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
2 |
|
|
4 |
9 |
|
|
|
|
| 1 |
9 |
|
|
|
|
3 |
|
|
|
| 2 |
|
1 |
|
|
|
|
6 |
8 |
|
| 3 |
|
|
3 |
8 |
|
|
|
1 |
2 |
| 4 |
|
|
|
|
|
|
|
|
|
| 5 |
6 |
7 |
|
|
|
4 |
3 |
|
|
| 6 |
|
6 |
7 |
|
|
|
|
4 |
|
| 7 |
|
|
|
3 |
|
|
|
|
1 |
| 8 |
|
|
|
|
5 |
7 |
|
|
|
だと後で矛盾が起きてしまう場合、
この2を一端外して、
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
|
|
|
4 |
9 |
|
|
|
|
| 1 |
9 |
|
|
|
|
3 |
|
|
|
| 2 |
|
1 |
|
|
|
|
6 |
8 |
|
| 3 |
|
|
3 |
8 |
|
|
|
1 |
2 |
| 4 |
|
|
|
|
|
|
|
|
|
| 5 |
6 |
7 |
|
|
|
4 |
3 |
|
|
| 6 |
|
6 |
7 |
|
|
|
|
4 |
|
| 7 |
|
|
|
3 |
|
|
|
|
1 |
| 8 |
|
|
|
|
5 |
7 |
|
|
|
リスト構造も
lst(1,2,0)=2
lst(1,2,1)=4
lst(1,2,2)=5
lst(1,2,3)=6
lst(1,2,4)=8
lst(1,2,5)=1
lst(1,2,6)=3
lst(1,2,7)=7
lst(1,2,8)=9
mx(1,2)=5
に戻さなければならないわけです。
そのために、一端外しておいた数字2も保存しておく必要があるのです。
もっとも、
lst(1,2,5)=1
lst(1,2,6)=3
lst(1,2,7)=7
lst(1,2,8)=9
については、数独の問題の条件から絶対に使うことはないわけですが、
最初から問題に入っている数字と自分で入れた数字を区別すると、
また、プログラムが複雑になりますので、区別しないで、
最初から問題に入っている数字をいじらないようにする工夫は、
別の方法で行います。
リスト構造を {2,4,5,6,8}と5個 とわざわざ5個を付ける理由は、
実際の運用は集合は{2,4,5,6,8,1,7,3,9}となっていて、
使用するのは、最初の5個
{2,4,5,6,8,1,3,7,9}
のみになっているからです。
ですから、セル(1,2)のリスト構造の正確な説明は
集合{2,4,5,6,8,1,3,7,9}と使用個数5個というということになります。
では、いよいよプログラムの開発に入ります。
本来リストの集合を表す配列lst(i, j, k)は3次元配列ですし、
また、リスト数を表すmxも2次元配列mx(i, j)でなければなりませんが、
いきなり全体セルリスト構造解析を考えたのでは複雑すぎますので、
当面はセル(1,2)の構造解析に限定するために
3次元配列lst(i, j, k)は1次元配列lst(k)に、
2次元配列mx(i, j)は変数mxに限定します。
まず、サンプルファイルをダブルクリックで開いて下さい。
そして、Alt+F11をしてVBAのコードをご覧下さい。
Dim mah(8, 8) As Byte, lst(8) As Byte, mx As Byte
Private Sub CommandButton1_Click()
dainyuu
syokika
cellkaiseki
hyouji
End Sub
Sub dainyuu()
End Sub
Sub hyouji()
End Sub
Sub syokika()
End Sub
Sub cellkaiseki()
End Sub
Private Sub CommandButton2_Click()
Range("B14", "J22").Select
Selection.ClearContents
Range("M5", "V9").Select
Selection.ClearContents
Cells(2, 1).Select
End Sub
このようにコードが空になっています。
皆さんにこれからコードを埋めていって頂きます。
まず、
Sub dainyuu()
End Sub
のコードから考えて頂きます。
配列mah(i, j)は、問題の数字と答えの数字を入れる配列です。
この配列に問題の数字を代入するのがdainyuuの役割です。
ただし、空欄になっているところは0を代入して下さい。
| |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0 |
|
|
|
4 |
9 |
|
|
|
|
| 1 |
9 |
|
|
|
|
3 |
|
|
|
| 2 |
|
1 |
|
|
|
|
6 |
8 |
|
| 3 |
|
|
3 |
8 |
|
|
|
1 |
2 |
| 4 |
|
|
|
|
|
|
|
|
|
| 5 |
6 |
7 |
|
|
|
4 |
3 |
|
|
| 6 |
|
6 |
7 |
|
|
|
|
4 |
|
| 7 |
|
|
|
3 |
|
|
|
|
1 |
| 8 |
|
|
|
|
5 |
7 |
|
|
|
ですから、
mah(0, 0) = 0
mah(0, 1) = 0
mah(0, 2) = 0
mah(0, 3) = 4
mah(0, 4) = 9
mah(0, 5) = 0
・
・
・
mah(1, 0) = 9
mah(1, 1) = 0
mah(1, 2) = 0
mah(1, 3) = 0
mah(1, 4) = 0
mah(1, 5) = 3
・
・
・
としたいわけです。
成功したかどうかを確認するために
Sub hyouji()
End Sub
のコードも入れましょう。
ですから、
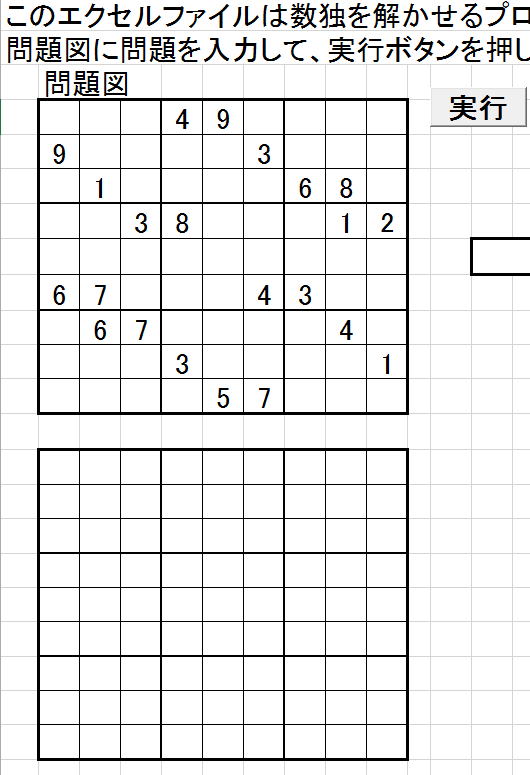
の状態から実行ボタンを押すと
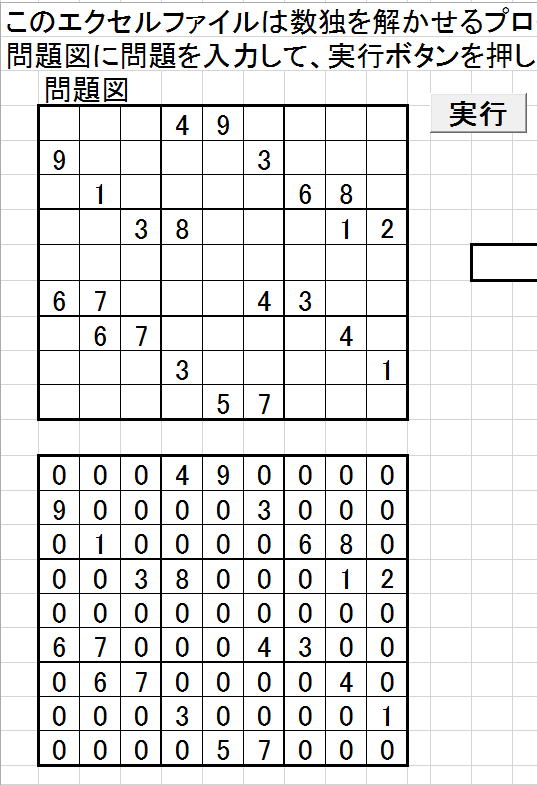
となるようにして頂きたいのです。
第1話へ 第3話へ

初心者のためのc++ vc++ c言語 入門 基礎から応用までへ
初心者のための excel 2007 2010 2013 vba マクロ 入門 基礎から応用まで
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
vb講義トップへ
VB講義基礎へ
専門用語なしのC++入門へ
専門用語なしのJava入門へ
専門用語なしのVBA入門
数独のページ
魔方陣のページ
数学研究室に戻る
本サイトトップへ


