第７話 動き方６通りからランダムに選ぶ
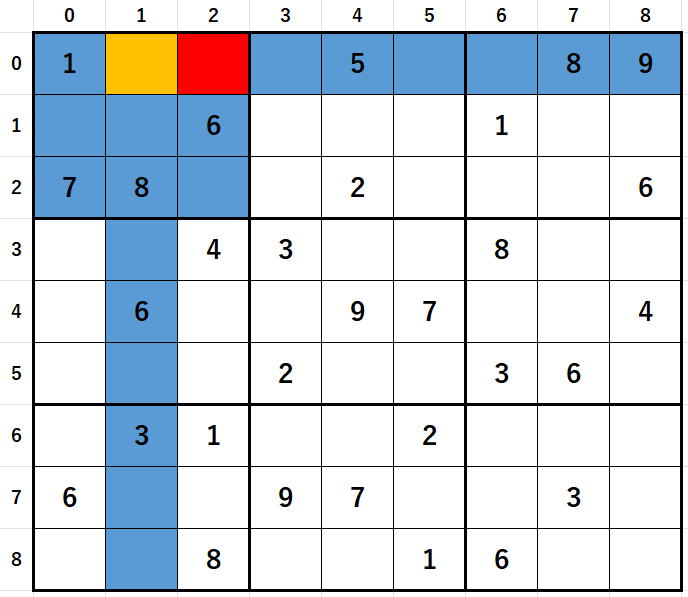
コード変更部分
Sub f(g As Byte, cn As Integer, n As Byte, x() As Byte)
Dim h As Byte, i As Byte, j As Byte, k As Byte, a As Byte, s As Integer, gi As Byte, gj As Byte
Dim ji As Byte, jj As Byte, hh As Byte, w As Byte, ii As Byte, iii As Byte, kk As Byte, kkk As Byte
a = cn Mod 10
s = Int(cn / 10)
gi = Int(g / n)
gj = g Mod n
ii = Int(n * Rnd)
kk = Int(6 * Rnd)
If kk = 0 Then kkk = 1
If kk = 1 Then kkk = 2
If kk = 2 Then kkk = 4
If kk = 3 Then kkk = 5
If kk = 4 Then kkk = 7
If kk = 5 Then kkk = 8
For i = 1 To n
iii = ((i - 1) * kkk + ii) Mod n
x(gi, gj) = iii + 1
・
・
・
なぜ、２重にランダム化しなければならないのでしょうか。
実は、ランダム要素を入れる前の、
一番最初に作られる
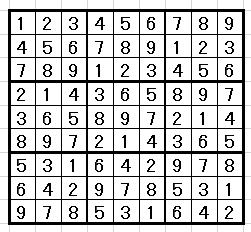から空欄を作って、数独の問題を作ったとします。
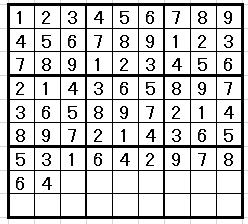
例えば上の問題です。
ところがヒント数が６６個もあっても、
解は複数存在してしまうのです。
この解答からヒント数２０などの問題を作るのは、
夢のまた夢といわなければなりません。
今回のプログラミングでわかったことは、
数独の解答を自動生成させることは、
とても簡単だということです。
適当に配置したのでは、
配置までが数独のルール
① 列に数字の重複がない
② 行に数字の重複がない
③ ブロックに数字の重複がない
を守ったとしても、９９％の確率で解のない問題になりますし、
幸運にも解のある問題だったとしても、
そのうちの９９．９％ぐらいは複数の答えを持つ問題になってしまうのです。
つまり、適当に配置したのでは多くても１／１０万分ぐらいの確率でしか、
数独の問題はできないのです。
これに理詰めのみで解けるという条件、
難問という条件を付け加えるならば、
適当に配置したのでは、１／１０００万分ぐらいの確率でしか数独はできません。
ですから、数独の問題を作るには、
解答側から空欄を作って作る方が簡単なのです。
ですが、解答の数字の並びによっては、
そこから数独問題を作り出すのは、
大変難しいのです。
それで、できるだけランダムな並びにする必要があるのです。
２重ランダムを取り入れている所以です。
すぐにも数独自動生成アプリの開発に取り組みたいところでしょうが、
まだまだ、クリアしなければならない課題があります。
粘り強くこの講義についてきて頂ければと思います。
さて、第13講は以上としまして、
第14講では、末項確定法による
魔方陣自動生成ソフトの高速化を図ります。
