第5話 魔方陣自動生成ソフトの完成!
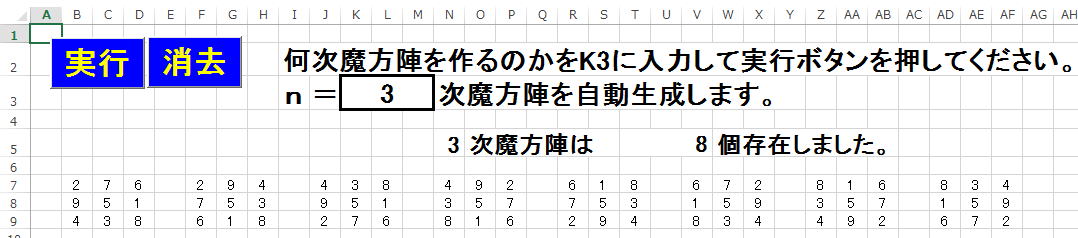
2次元配列による方陣順列の行と列の合計を一致させるコード例
Private Sub CommandButton1_Click()
Dim n As Byte, cn As Integer, x(10, 10) As Byte
Rows("5").Select
Selection.ClearContents
Range("A1").Select
n = Cells(3, 11)
cn = 0
Call f(0, cn, n, x())
Cells(5, 14) = n
Cells(5, 15) = "次魔方陣は"
Cells(5, 20) = cn
Cells(5, 23) = "個存在しました。"
End Sub
Sub f(g As Byte, cn As Integer, n As Byte, x() As Byte)
Dim h As Byte, i As Byte, j As Byte, k As Byte, a As Byte, s As Integer, gi As Byte, gj As Byte
Dim ji As Byte, jj As Byte, hh As Byte, w As Byte
a = cn Mod 10
s = Int(cn / 10)
gi = Int(g / n)
gj = g Mod n
For i = 1 To n * n
x(gi, gj) = i
h = 1
If g > 0 Then
For j = 0 To g - 1
ji = Int(j / n)
jj = j Mod n
If x(ji, jj) = x(gi, gj) Then
h = 0
Exit For
End If
Next
End If
If h = 1 Then
If gj = n - 1 Then
w = 0
For j = 0 To n - 1
w = w + x(gi, j)
Next
If w <> Int(n * (n * n + 1) / 2) Then h = 0
End If
End If
If h = 1 Then
If gi = n - 1 Then
w = 0
For j = 0 To n - 1
w = w + x(j, gj)
Next
If w <> Int(n * (n * n + 1) / 2) Then h = 0
End If
End If
If h = 1 Then
If gi = n - 1 And gj = 0 Then
w = 0
For j = 0 To n - 1
w = w + x(j, n - 1 - j)
Next
If w <> Int(n * (n * n + 1) / 2) Then h = 0
End If
End If
If h = 1 Then
If gi = n - 1 And gj = n - 1 Then
w = 0
For j = 0 To n - 1
w = w + x(j, j)
Next
If w <> Int(n * (n * n + 1) / 2) Then h = 0
End If
End If
If h = 1 Then
If g + 1 < n * n Then
Call f(g + 1, cn, n, x())
Else
For j = 0 To n - 1
For k = 0 To n - 1
Cells(7 + j + (n + 1) * s, 2 + k + (n + 1) * a) = x(j, k)
Next
Next
cn = cn + 1
End If
End If
Next
End SubPrivate Sub CommandButton2_Cl
参考ファイル
解説
If h = 1 Then
If gi = n - 1 And gj = 0 Then
w = 0
For j = 0 To n - 1
w = w + x(j, n - 1 - j)
Next
If w <> Int(n * (n * n + 1) / 2) Then h = 0
End If
End If
If h = 1 Then
If gi = n - 1 And gj = n - 1 Then
w = 0
For j = 0 To n - 1
w = w + x(j, j)
Next
If w <> Int(n * (n * n + 1) / 2) Then h = 0
End If
End If
