第7話 転置行列の表示も1次元For文で行う!
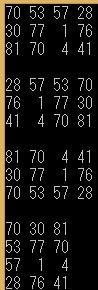
の転置行列の表示も1次元For文で実点するコード例
Module Module1
Sub Main() '私は社長だ。
'Rnd(-1)
'Randomize(Timer())
f()
End Sub
Sub f()
Dim a(11) As Integer '配列aの宣言
Dim i As Integer
'ランダムデータ生成
For i = 0 To 11
a(i) = Int(Rnd() * 100)
Next
'データ表示
For i = 0 To 11
If i > 0 And (i Mod 4) = 0 Then Console.WriteLine() '改行
If a(i) < 10 Then Console.Write(" {0:d} ", a(i))
If a(i) >= 10 Then Console.Write("{0:d} ", a(i))
Next
Console.WriteLine() '改行
Console.WriteLine() '改行
'左右反転行列の表示
For i = 0 To 11
If i > 0 And (i Mod 4) = 0 Then Console.WriteLine() '改行
If a(4 * Int(i / 4) + (3 - (i Mod 4))) < 10 Then Console.Write(" {0:d} ", a(4 * Int(i / 4) + (3 - (i Mod 4))))
If a(4 * Int(i / 4) + (3 - (i Mod 4))) >= 10 Then Console.Write("{0:d} ", a(4 * Int(i / 4) + (3 - (i Mod 4))))
Next
Console.WriteLine() '改行
Console.WriteLine() '改行
'上下反転行列の表示
For i = 0 To 11
If i > 0 And (i Mod 4) = 0 Then Console.WriteLine() '改行
If a(8 - 4 * Int(i / 4) + (i Mod 4)) < 10 Then Console.Write(" {0:d} ", a(8 - 4 * Int(i / 4) + (i Mod 4)))
If a(8 - 4 * Int(i / 4) + (i Mod 4)) >= 10 Then Console.Write("{0:d} ", a(8 - 4 * Int(i / 4) + (i Mod 4)))
Next
Console.WriteLine() '改行
Console.WriteLine() '改行
'転置行列の表示
For i = 0 To 10
If i > 0 And (i Mod 3) = 0 Then Console.WriteLine() '改行
If a(4 * i Mod 11) < 10 Then Console.Write(" {0:d} ", a(4 * i Mod 11))
If a(4 * i Mod 11) >= 10 Then Console.Write("{0:d} ", a(4 * i Mod 11))
Next
If a(11) < 10 Then Console.Write(" {0:d} ", a(11))
If a(11) >= 10 Then Console.Write("{0:d} ", a(11))
Console.WriteLine() '改行
End Sub
End Module
解説
0,4,8,12,16,20,24,28,32,36,40
を11で割った余りを求めると、
0,4,8,1,5,9,2,6,10,3,7
になります。
この手法を是非頭に刻んで下さい。
将来テトリスなどを開発するときに、
活かせる手法です。
私の数独作成ソフトにおいても、
ヒントになる数字を配置するときに使っています。
数独作成においては
For i = 0 To h - 1 'hはヒント数
g= p*i Mod 80
y(i) = Int(g / 9)
x(i) = g Mod 9
Next
のようにして座標を設定してヒントとなる数字を配置しています。
80で割った余りになっているのは、
プログラミングの世界では普通0からカウントし、
80が81番目になるからです。
9×9=81マスの数字を埋めて行くのが数独(ナンプレ)ですよね。
さて、次話では3次元配列と1次元配列の関係を考えます。
第6話へ 第8話へ

初心者のための excel 2016 マクロ VBA 入門講義 基礎から応用まで
vc++ c言語 c++ 入門 初心者 基礎から応用まで
eclipse c++ 入門
魔方陣 数独で学ぶ VBA 入門
数独のシンプルな解き方・簡単な解法の研究
VB講義へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための世界で一番わかりやすいVBA入門講義(基礎から応用まで)
初心者のための VC++による C言語 C++ 入門 基礎から応用まで第1部
eclipse java 入門
java 入門 サイト 基礎から応用まで
本サイトトップへ