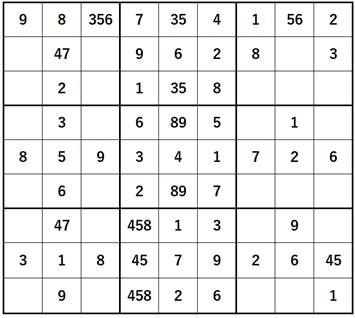
自然数nに対して、
 を
を で表す。たとえば
で表す。たとえば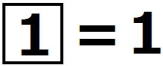 ,
,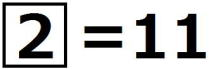 ,
,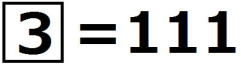 である。
である。(1) mを0以上の整数とする。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。(1)の超解説その7((1)の解答の肝その2)
その6では、
第2問 2008年度 東大数学 理系 第5問
自然数nに対して、 を
を で表す。たとえば
で表す。たとえば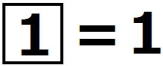 ,
,
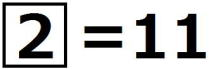 ,
,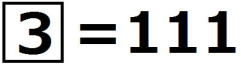 である。
である。
(1) mを0以上の整数とする。![]() は
は![]() で割り切れるが、
で割り切れるが、
![]() では割り切れないことを示せ。
では割り切れないことを示せ。
(2) nが27で割り切れることが、
 が27で割り切れるための必要十分条件であることを示せ。
が27で割り切れるための必要十分条件であることを示せ。
(1)の超解説その7((1)の解答の肝その2)
その6では、
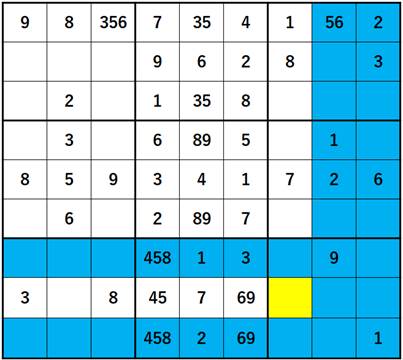
|
(1)の命題を(*)とし、(*)が成り立つことを数学的帰納法で示す。 ⅰ m=0のとき、  =1 =1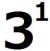 =3 =3したがって、 (*)は成り立つ。 ⅱ m=k(≧0)とき(*)が成り立つと仮定すると、  は は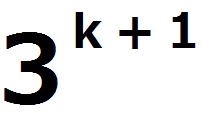 では割り切れないから、 では割り切れないから、3で割り切れない適当な整数pが存在して、  =p =pm=k+1の場合を考える。 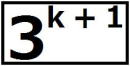 = = =  = 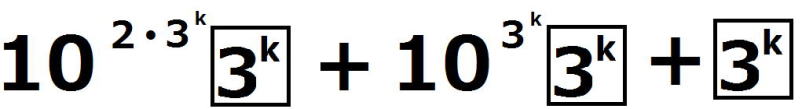 |
まで超解説しました。その7では
=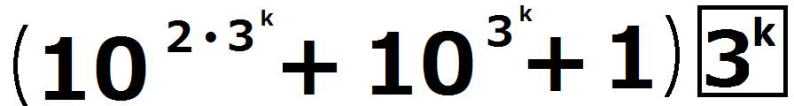 ここで、 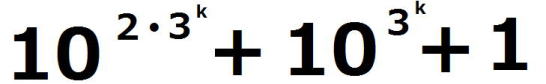 の各位の数字の和は3なので、 の各位の数字の和は3なので、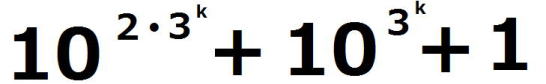 は3の倍数であるが、9の倍数ではない。 は3の倍数であるが、9の倍数ではない。よって、3で割り切れない整数qによって 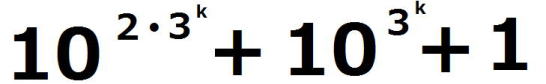 =3q =3qとおける。このとき 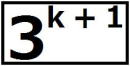 =3q・p =3q・p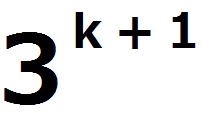 p,qは3の倍数でないので、適当な整数a,bによって、 p=3a±1,q=3b±1 と表せる。4つの組み合わせ pq=3(3ab+a+b)+1,3(3ab-a+b)-1,3(3ab+a-b)-1,3(3ab-a-b)+1 はいずれも3の倍数ではない。 したがって、 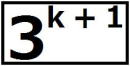 は は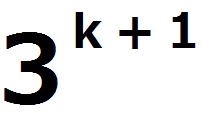 で割り切れるが、 で割り切れるが、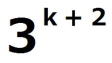 では割り切れないから、 では割り切れないから、(*)はm=k+1の場合も成り立つ。 以上ⅰⅱより、0以上のすべての整数について(*)が成り立つことが証明された。 |
の部分を超解説します。
まず、
=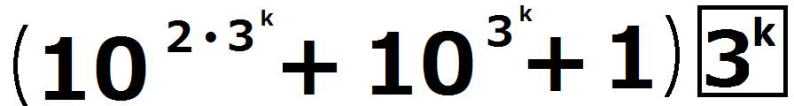
は
=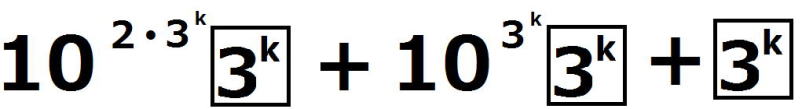
の を共通因数として括弧にくくっただけです。
を共通因数として括弧にくくっただけです。
ここで、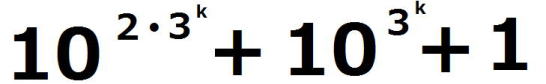 の各位の数字の和は3なので、
の各位の数字の和は3なので、
これどうしてですか。
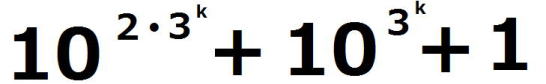 は
は
すなわち、

です。
ですから、1+0+0+0+・・・+0+0+1+0+0+0+・・・+0+0+1から、
各位の数字の和は3という訳です。
難解に見えても具体化すると、数学の苦手な方でもわかりやすいのではないですか。
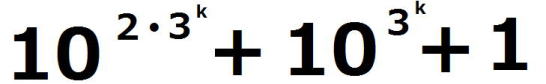 だとなんだか分からなくても、
だとなんだか分からなくても、

なら各位の数字の和が3であることは自明です。
私が、『右脳数学と魔方陣』というサイトを立ち上げた最大の理由は、
現在の数学教育は抽象一辺倒になっていて、具体的なものがイメージできないようになっているということです。
抽象一辺倒は、論理一辺倒・形式一辺倒・左脳一辺倒と言い換えてもいいものです。
抽象・論理・形式・左脳の反対語はそれぞれ具体・直観(イメージ)・内容・右脳です。
現代の数学教育は、左脳一辺倒になり具体・直観(イメージ)・内容が抜け落ちてしまっているのです。
ヘーゲルはいっています。
『常に普遍的なものは個別的であり、個別的なものは普遍的である。』
普遍的なものすなわち抽象的なものは具体的なものを包摂しています。
抽象を見るとき、そこに具体が見えないなら、
本当の数学学習ではありません。
その逆、具体の中に抽象的なもの=一般的なものが見えないなら、
真の数学学習ではありません。
正しい数学学習は、具体と抽象の世界を常に行ったり来たりすることです。
具体と抽象は、数学というより学問一般の車の両輪です。
ところが、現代の数学教育は抽象一辺倒の片輪走行=片肺走行になってしまっています。
生徒には、抽象的なもの以外何も見えなくなってしまっています。
抽象に具体を見、具体に抽象を見るが正しい数学学習、学問学習なのです。
この講義が超解説を採用する所以です。
話を元に戻しましょう。
 の各位の数字の和は、
の各位の数字の和は、
3です。ですから、これは3の倍数ですが9の倍数ではありません。
3の倍数は各位の数字の和が3の倍数であり、
9の倍数は各位の数字の和が9の倍数でしたね。
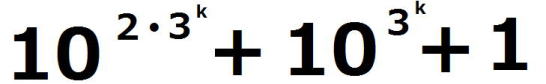 が3の倍数で9の倍数ではないので、
が3の倍数で9の倍数ではないので、
3の倍数でない自然数qによって、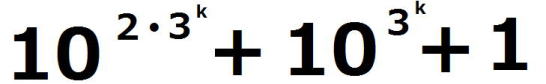 は
は
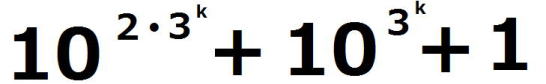 =3q
=3q
を表せるわけです。qをわざわざ3の倍数でないと断っている理由は、
もし3の倍数であるとすると
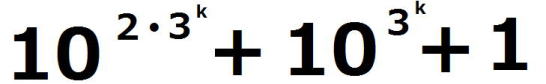 が9の倍数でなくなってしまうからです。
が9の倍数でなくなってしまうからです。
さて、
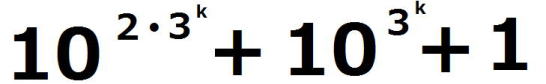 =3q
=3q
と
 =p
=p![]()
とから
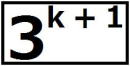 =3q・p
=3q・p![]() =pq
=pq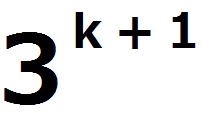
となります。pも3の倍数でないと断ってありましたね。
ここでpqが3の倍数でなければ、
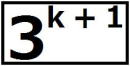 は
は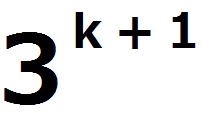 の倍数ですが、
の倍数ですが、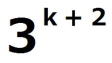 の倍数でないことが分かります。
の倍数でないことが分かります。
もし、pqが3の倍数であるとするともうひとつ3が増えてしまい、
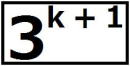 は
は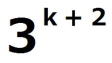 の倍数ということになってしまいます。
の倍数ということになってしまいます。
p,qは3の倍数でないので、適当な整数a,bによって、
p=3a±1,q=3b±1
と表せる。4つの組み合わせ
pq=3(3ab+a+b)+1,3(3ab-a+b)-1,3(3ab+a-b)-1,3(3ab-a-b)+1
はいずれも3の倍数ではない。
のところは、3の倍数でないもの同士をかけるとやはり3の倍数でないことを証明しています。
したがいまして、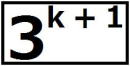 は
は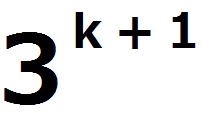 では割り切れますが、
では割り切れますが、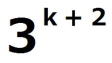 では割り切れないことになり、
では割り切れないことになり、
(*)はm=k+1でも成り立つことになります。
以上で数学的帰納法の要件が満たされ命題(*)が示されたわけです。
(1)の解答超解説その6へ (2)の解答へ

数独 フリーソフト 数独自動生成無料アプリ 難問 作成 プログラム
魔方陣 数独で学ぶ 初心者のための VBA 入門 基礎から応用まで
数独 ナンプレ 難問 シンプルな解き方・簡単な解法・わかりやすい攻略法の研究
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第2部
初心者のための
VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のためのEclipseによるJava入門 基礎から応用まで
初心者のためのJava入門サイト 基礎から応用まで
本サイトトップへ