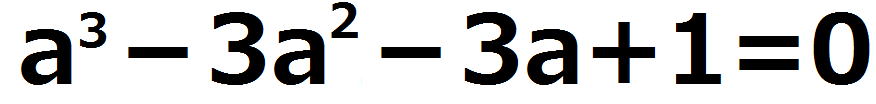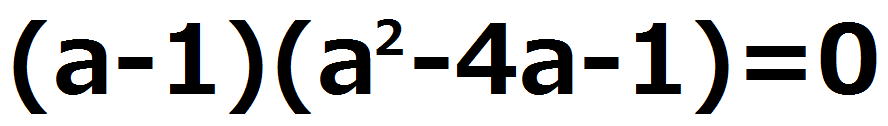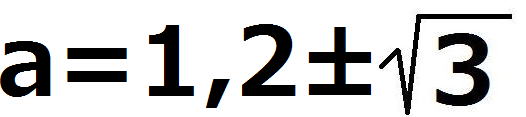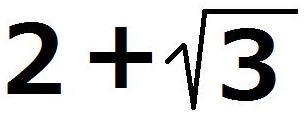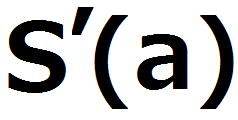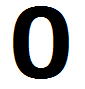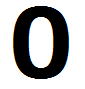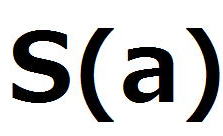第1問 2011年度 東大数学 理系 第1問(2)
(2012年3月10日全国紙ベネッセ1面広告問題
ベネッセによる1部加筆あり)
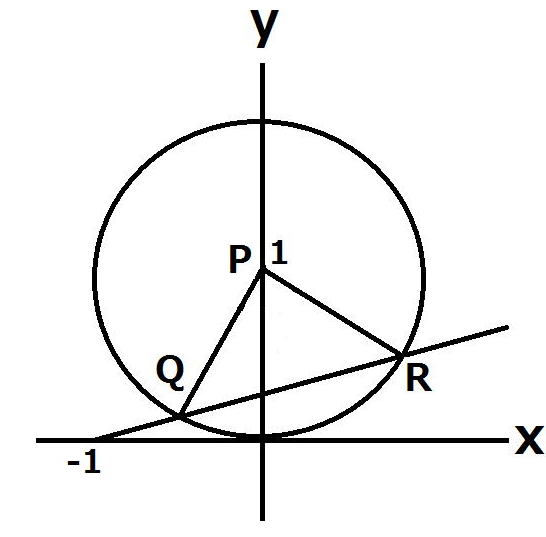
座標平面において、点P(0,1)を中心とする半径1の円をCとする。
aを0<a<1を満たす実数とし、
直線y=a(x+1)とCとの交点をQ、Rとする。
aが0<a<1の範囲を動くとき、△PQRの面積S(a)が最大となるaを求めよ。
解法その1(数Ⅲの「微分」による解法その1)
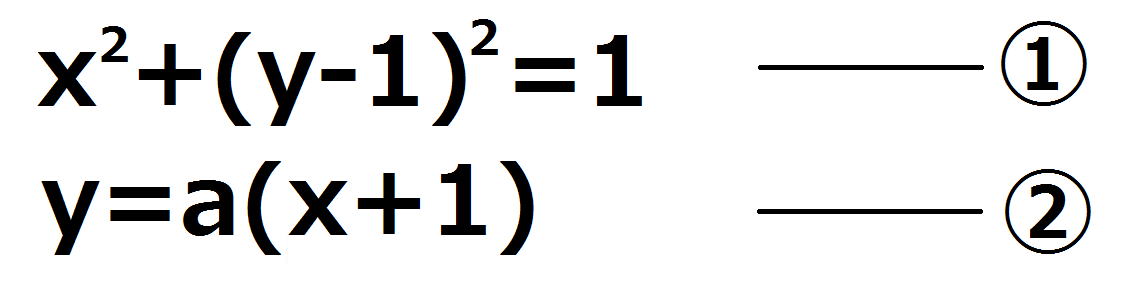
②を①に代入して整理すると、
Qのx座標をα、Pのx座標をβとすると、解と係数の関係から、
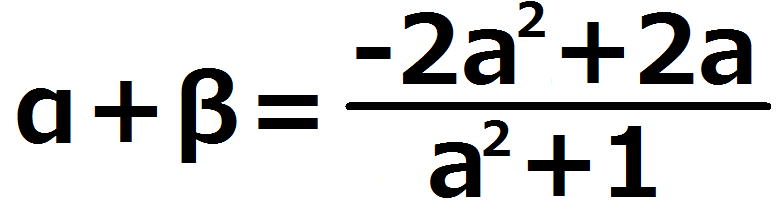
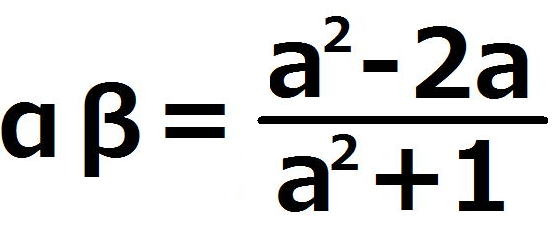
(α+β)の2乗-4αβを計算して、
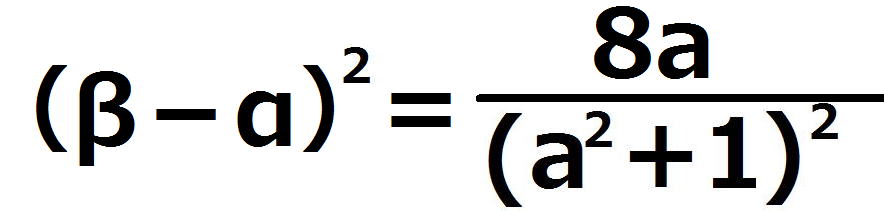
β-α>0より
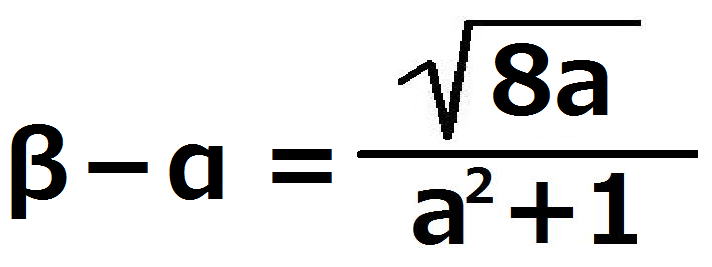
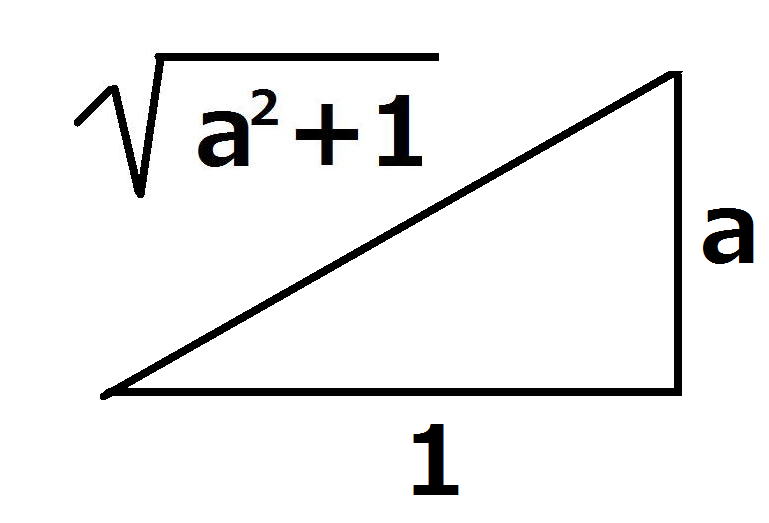 より
より
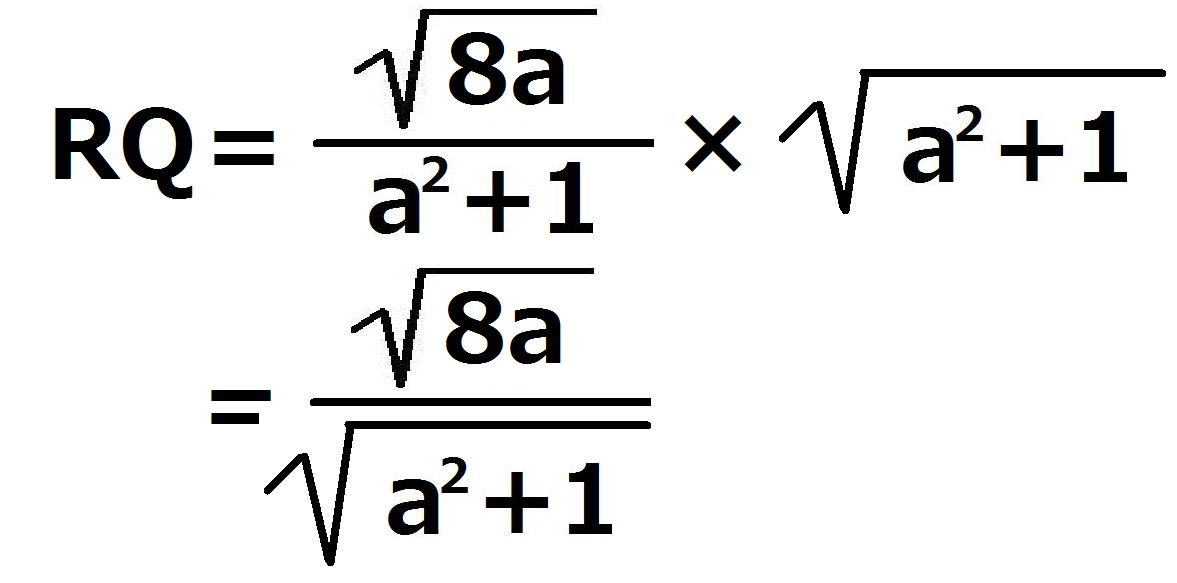
一方、y=a(x+1)からax-y+a=0であるから、点Pと直線RQの距離は、
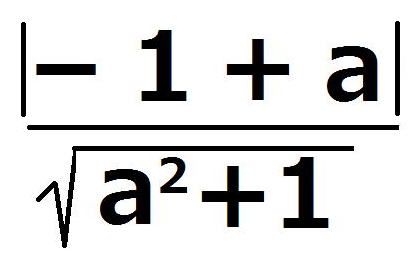
したがって、
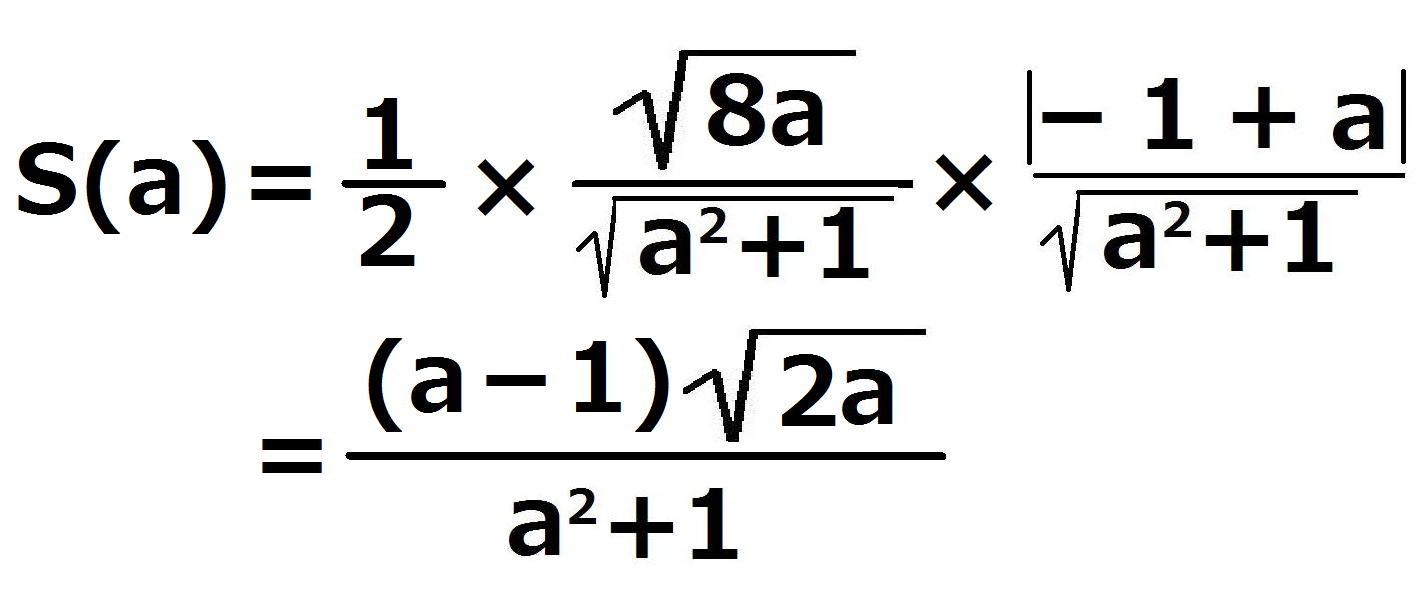
この両辺をaで微分すると、
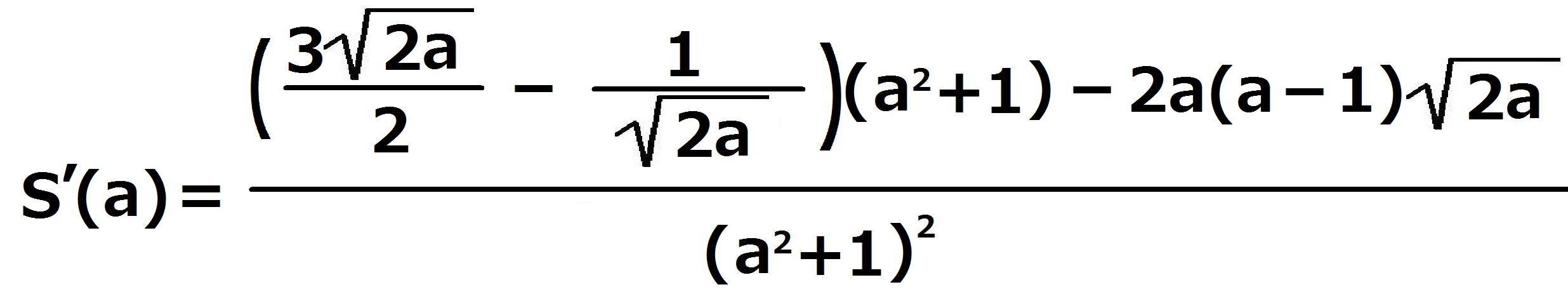
s’(a)=0とおいて、両辺に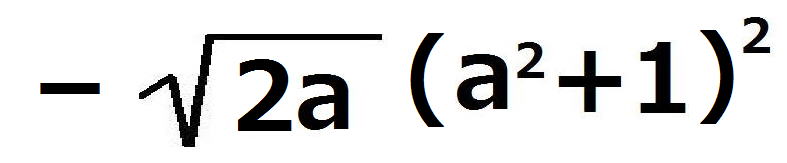 をかけると、
をかけると、
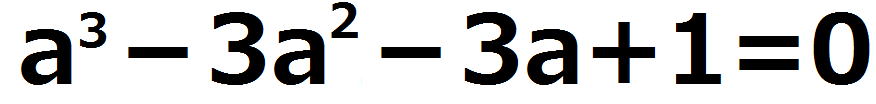
因数定理を利用して因数分解して、
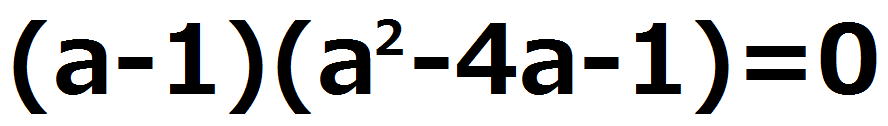
ゆえに、3次方程式の解は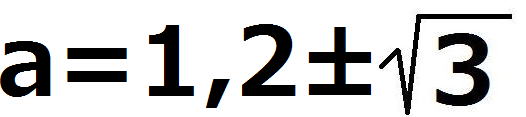
増減表は
以上より、S(a)を0<a<1の範囲で最大にするaは
美しい解答へ

数独 ナンプレ 解き方 コツ 解法 難問 テクニック 研究
数独 フリーソフト 数独自動生成無料アプリ 難問 作成 プログラム
魔方陣 数独で学ぶ 初心者のための VBA 入門 基礎から応用まで
数独 ナンプレ 難問 シンプルな解き方・簡単な解法・わかりやすい攻略法の研究
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門
基礎から応用まで第2部
初心者のための
VC++による C言語 入門 C++ 入門 基礎から応用まで第3部
初心者のためのEclipseによるJava入門 基礎から応用まで
初心者のためのJava入門サイト 基礎から応用まで
本サイトトップへ

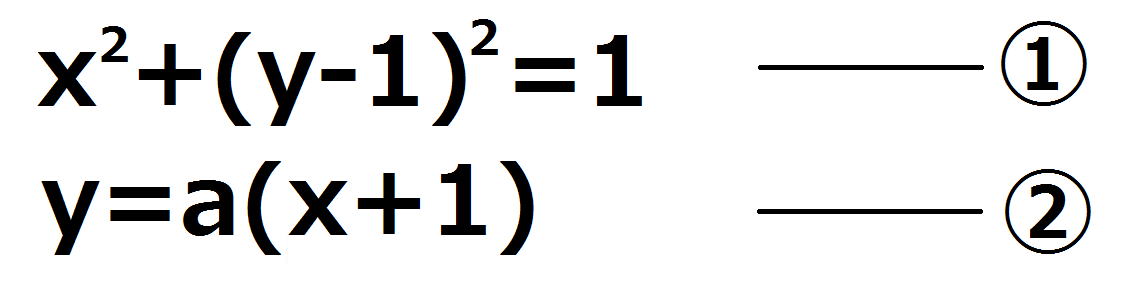

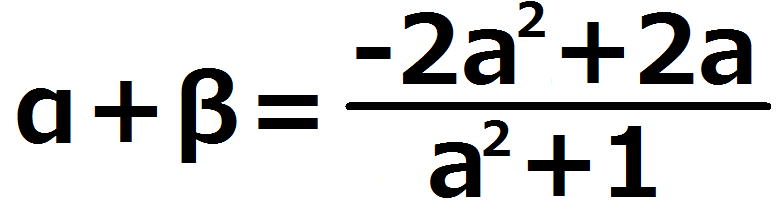
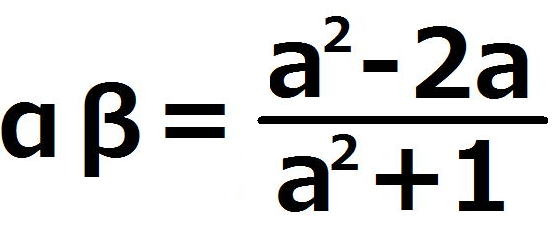
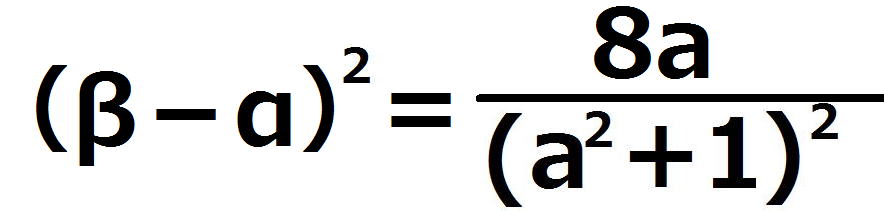
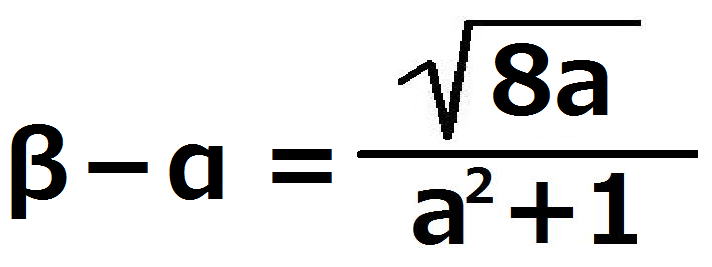
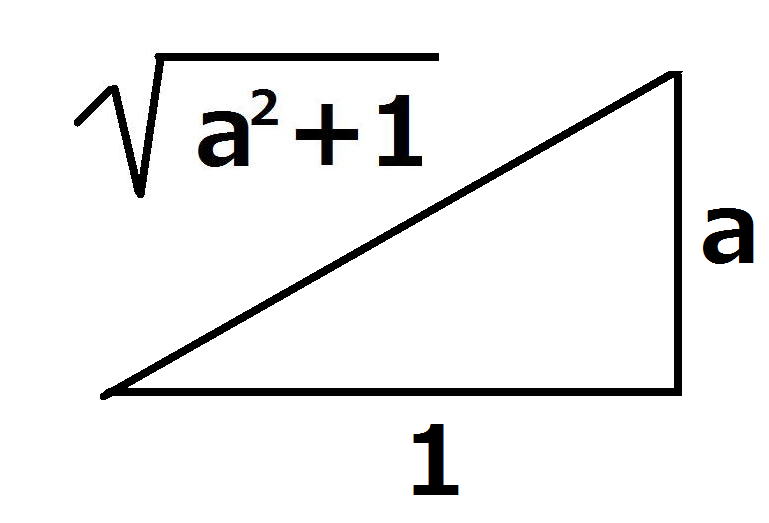 より
より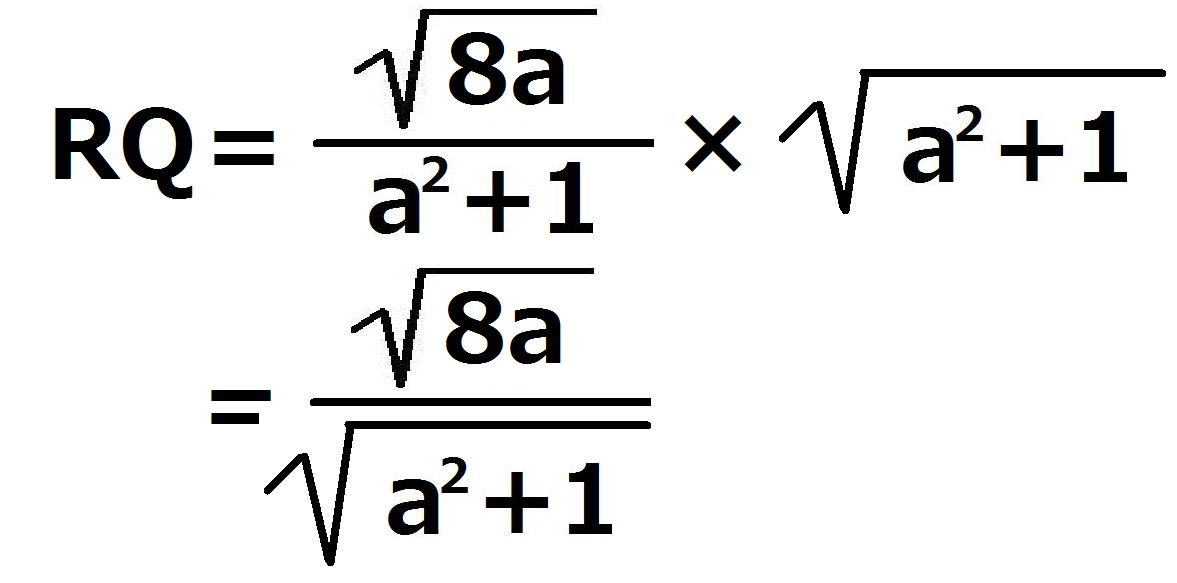
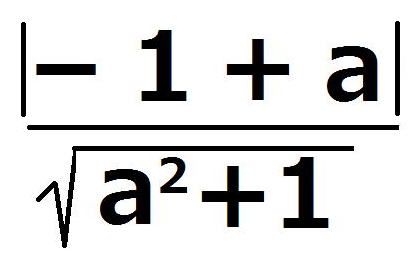
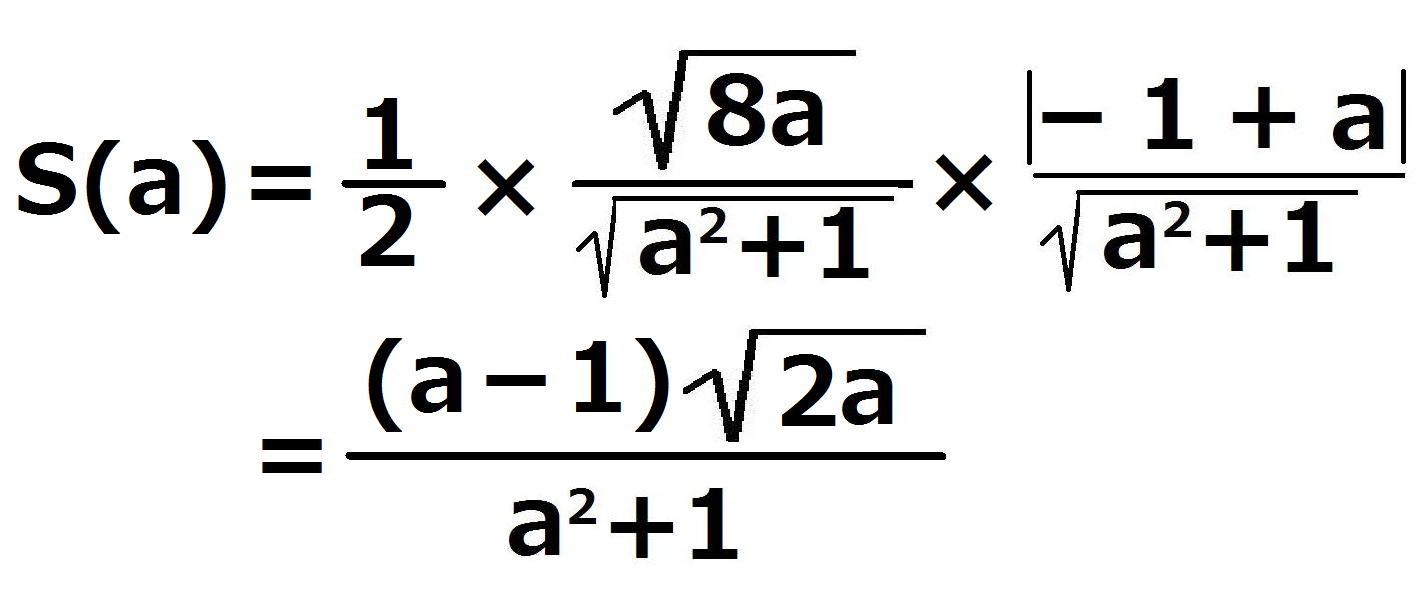
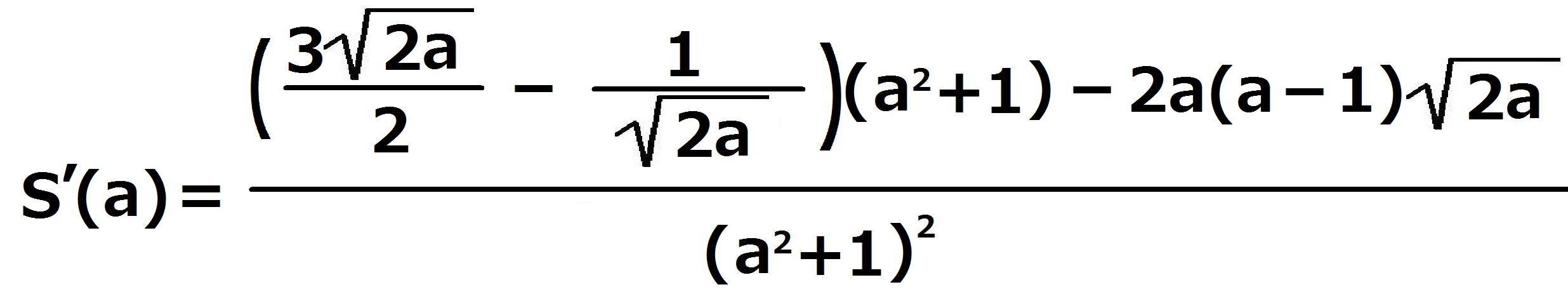
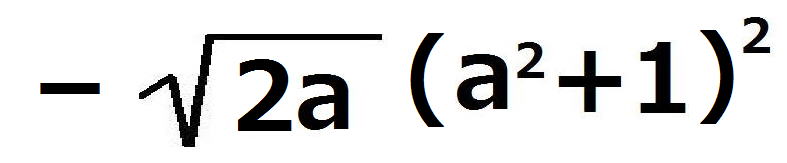 をかけると、
をかけると、