第８話　リボン計算（リボン演算）の証明
　　　　

NEKOは
大好きな先生のアドバイスに従い、
証明に取り組みました。
数学が苦手だったNEKOにはちょっと重い課題でしたが、
がんばったのです。
一生懸命考えました。
にゃにしたらいいの〜
NEKOは、体をなめなめしてお掃除しながら考えたのです。
無意識にしっぽも振っていました。
すると、にゃんとすばらしいアイデアが浮かびました。
確か中学生のときに、
２桁の整数は整数ａ，ｂを使って１０ａ＋ｂと
表せると習ったことを思い出したのです。
これに気がつけば証明は後一歩です。

２桁同士のかけ算がリボン計算（リボン演算）でできることの証明
ａとｃを１以上９以下の任意の整数、
ｂとｄを０以上９以下の任意の整数とすると、
２つの２桁の整数は、それぞれ
１０ａ＋ｂ
１０ｃ＋ｄ
と表せる。
このとき、２つの整数の積は
　（１０ａ＋ｂ）（１０ｃ＋ｄ）

＝１００ａｃ＋１０（ａｄ＋ｂｃ）＋ｂｄ

よって、リボン計算（リボン演算）が成り立つことが証明された。


そうです。
リボン計算（リボン演算）は、中学生に証明できるのです。
(といっても、中学生にとっては簡単な証明とはいえませんが。)


　（１０ａ＋ｂ）（１０ｃ＋ｄ）

＝１００ａｃ＋１０（ａｄ＋ｂｃ）＋ｂｄ

は誰でも知っていることです。

例えば、３７×２３は、

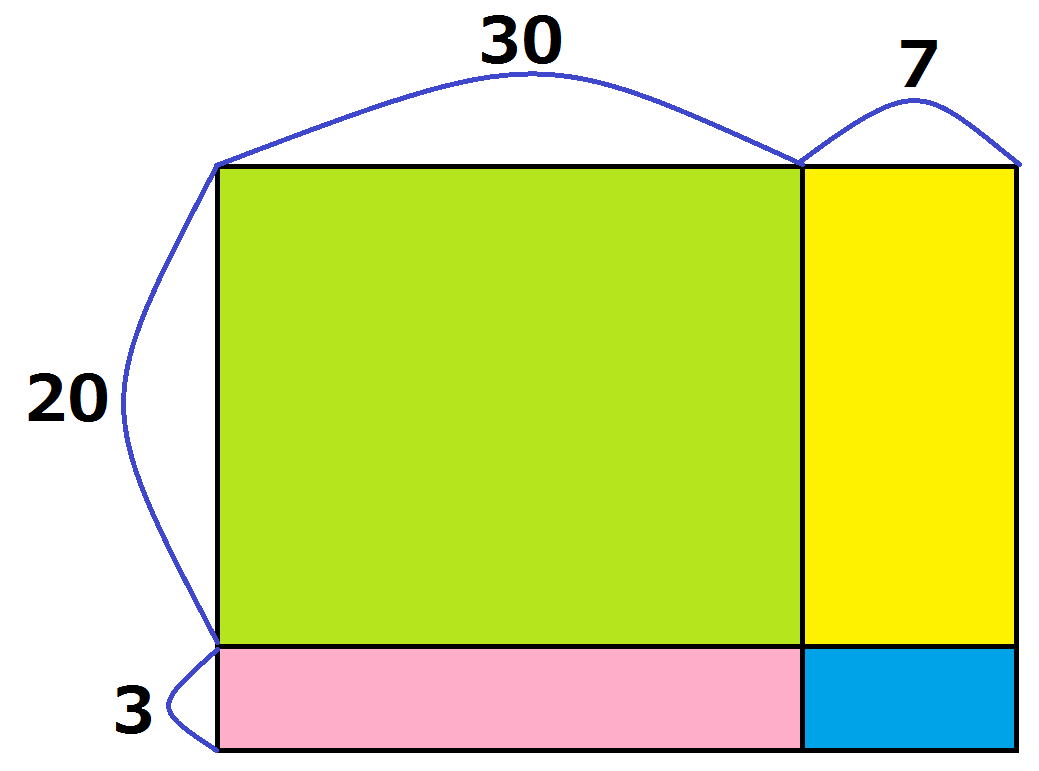
３０×２０＋７×３＋３０×３＋２０×７
です。
ですからリボン計算（リボン演算）の原理は、
小学生にも理解できるほど簡単です。

でも、現時点でもリボン計算（リボン演算）は
小学校の算数教育に取り入れられていません。
取り入れた方が、
計算力をアップさせることができることは明らかです。
ひょとしたら一部の学校では、取り入れている学校もあるかもしれませんが、
全国のほとんどの小学校では取り入れられていないでしょう。
このコーナーのトップにも書いたとおり、
おそらくＮＥＫＯの発見は再発見でしょう。
しかし、その発見の意義を正当に評価してこなかったことは確実です。
正当に評価するなら、
算数の教科書に入れるべきだからです。
そして、全国津々浦々でリボン計算（リボン演算）による暗算を取り入れるべきです。
一昔前に流行った１００ます計算で学力が伸びるは真実ではありませんが、
２桁暗算１００ます計算を実践すれば、
小学生の計算力が飛躍的に増大することは明らかです。
そして、認知症予防ドリルとして売り出せば認知症の予防にもなるはずです。

原理が簡単ということと気がつくということは、
別のことです。
真理とは、簡単なことである場合が多いのです。
でも、ほとんどの場合
目の前に落ちている原石に気がつかない、
ということも事実です。
私たちは、簡単な真理を見落としている！
のです。
ＮＥＫＯは原石を拾いました。
その原石を磨いて宝石に変えるのは、
我々教育者の責務です。
ＮＥＫＯのすばらしい発見を正当に評価して、
算数の教科書に入れて、
少しでも算数嫌いが減るようにしようではありませんか。



第７話へ　第９話へ

初心者のためのjava 入門 基礎から応用まで
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第１部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第２部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第３部
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座へ
VC++入門
VBA入門
専門用語なしのVBA入門
VB入門
初心者のためのEclipseによるJava入門